puzzle1012战舰

puzzle(1012)战舰
目录
一,战舰
找出藏在格子里的战船的位置,有些战船已经部分被揭示。
战船是一条连续不断的由黑方块组成的直线,各种大小的战船的数量显示在格子下方的提示里。
两条战船不能相邻(包括斜向),格子旁边的数字显示该行/列中被战船占据的格子数量。
6*6


隐藏规则
长为1的战舰由1个圆组成,长大于1的战舰除了两边的格子中间的都是正方形。
每个一共是三种不同的格子,初始局面给出的格子是哪一种是明确的。
8*8


39战舰(3)82(6)
中的关卡,下同。
39战舰(3)

答案:

82(6)
首先

分析左边2列发现,只能是下面的情况(其实还有一种等价的情况,就是把第4行和第六行交换)

所以答案就很明显了

120战舰(9)144(10)167(12)186(15)205(18)221(21)
规则和39战舰(3)82(6)一样,但是从66变成了1010,比较复杂了。
120战舰(9)

我干脆写了一个程序来计算答案。
代码:
#include<iostream>
using namespace std;
需要硬编码的 3 行///
const int m4 = 2, m3 = 2, m2 = 3, m1 = 3; //战舰的个数,m4=2 代表有 2 个长度为 4 的战舰
int line[nn] = { 2, 3, 2, 0, 5, 1, 0, 6, 2, 2 }; //列和
int row[nn] = { 1, 3, 1, 1, 4, 1, 5, 1, 2, 4 }; //行和
需要硬编码的 3 行///
const int nn = 10; //游戏的维度
int avail[nn][nn]; //能否放战舰,一个是战舰不相邻的问题,一个是游戏开始的障碍物问题
int out[nn][nn];
void save(int avail[nn][nn], int line[nn], int row[nn], int save_avail[nn][nn], int save_line[nn], int save_row[nn]) //保存 3 个数组
{
for (int i = 0; i < nn; i++)
{
for (int j = 0; j < nn; j++)save_avail[i][j] = avail[i][j];
save_line[i] = line[i];
save_row[i] = row[i];
}
}
void re(int save_avail[nn][nn], int save_line[nn], int save_row[nn], int avail[nn][nn], int line[nn], int row[nn]) //还原 3 个数组
{
for (int i = 0; i < nn; i++)
{
for (int j = 0; j < nn; j++)avail[i][j] = save_avail[i][j];
line[i] = save_line[i];
row[i] = save_row[i];
}
}
bool g(int n);
bool f(int n, int l) //n 是递归深度,也是放了多少个战舰,l 是战舰长度
{
for (int pr = 0; pr < nn; pr++) //横着放
{
for (int pl = 0; pl + l <= nn; pl++) //(pr,pl)是战舰的最左那个格子
{
bool f = false;
for (int k = pl; k < pl + l; k++)if (avail[pr][k] == 0)f = true;
if (f)continue;
int save_avail[nn][nn]; //回溯的时候保存avail
int save_line[nn];
int save_row[nn];
save(avail, line, row, save_avail, save_line, save_row);
row[pr] -= l;
if (row[pr] < 0)
{
re(save_avail, save_line, save_row, avail, line, row); //还原
continue;
}
f = false;
for (int k = pl; k < pl + l; k++)
{
line[k]--;
if (line[k] < 0)f = true;
}
if (f)
{
re(save_avail, save_line, save_row, avail, line, row);
continue;
}
for (int i = pr - 1; i <= pr + 1; i++)
{
if (i < 0 || i >= nn)continue;
for (int j = pl - 1; j <= pl + l; j++)
{
if (j<0 || j >= nn)continue;
avail[i][j] = 0;
}
}
if (g(n + 1))
{
for (int k = pl; k < pl + l; k++)out[pr][k] = 1;
return true;
}
else re(save_avail, save_line, save_row, avail, line, row);
}
}
for (int pr = 0; pr + l <= nn; pr++) //竖着放
{
for (int pl = 0; pl < nn; pl++) //(pr,pl)是战舰的最上那个格子
{
bool f = false;
for (int k = pr; k < pr + l; k++)if (avail[k][pl] == 0)f = true;
if (f)continue;
int save_avail[nn][nn]; //回溯的时候保存avail
int save_line[nn];
int save_row[nn];
save(avail, line, row, save_avail, save_line, save_row);
line[pl] -= l;
if (line[pl] < 0)
{
re(save_avail, save_line, save_row, avail, line, row);
continue;
}
f = false;
for (int k = pr; k < pr + l; k++)
{
row[k]--;
if (row[k] < 0)f = true;
}
if (f)
{
re(save_avail, save_line, save_row, avail, line, row);
continue;
}
for (int i = pr - 1; i <= pr + l; i++)
{
if (i < 0 || i >= nn)continue;
for (int j = pl - 1; j <= pl + 1; j++)
{
if (j<0 || j >= nn)continue;
avail[i][j] = 0;
}
}
if (g(n + 1))
{
for (int k = pr; k < pr + l; k++)out[k][pl] = 1;
return true;
}
else re(save_avail, save_line, save_row, avail, line, row);
}
}
return false;
}
bool g(int n) //控制调用顺序
{
if (n <= m4)return f(n, 4);
else if (n <= m4 + m3)return f(n, 3);
else if (n <= m4 + m3 + m2)return f(n, 2);
else if (n <= m4 + m3 + m2 + m1)return f(n, 1);
return true;
}
int main()
{
for (int i = 0; i < nn; i++)
{
for (int j = 0; j < nn; j++)
{
avail[i][j] = 1; //初始化,1 表示可以放,0 表示不可以
out[i][j] = 0;
}
}
g(1);
for (int i = 0; i < nn; i++)
{
for (int j = 0; j < nn; j++)cout << out[i][j] << " ";
cout << endl;
}
cout << "end";
system("pause>nul");
return 0;
}在最前面有 3 行是需要硬编码的,其他地方就固定不变了。

144(10)
规则和上面的差不多,唯一的区别是,有些格子开始的时候就不能放战舰,那么只需要在 main 函数里面对 avail 数组进行初始化的时候把这些格子对应的初始化为 0 就可以了。

167(12)

186(15)

205(18)

221(21)
这一关因为 m3 和 m2 比较大,所以运行的时候重复的情况比较严重,所以运行时间比较长。

二,扫雷战舰
12 战舰(1)54(4)95(7)161(11)180(14)199(17)216(20)
12 战舰(1)


这个游戏,规则确实和 很像,而且也很简单
答案:

54(4)

答案:

95(7)
答案:

161(11)
有唯一解
首先可以确定:

接着可以确定:

最后可以得到唯一解:

180(14)
答案:

199(17)
答案:

216(20)
答案:

三,边框战舰
24 战舰(2)69(5)107(8)174(13)193(16)211(19)227(22)
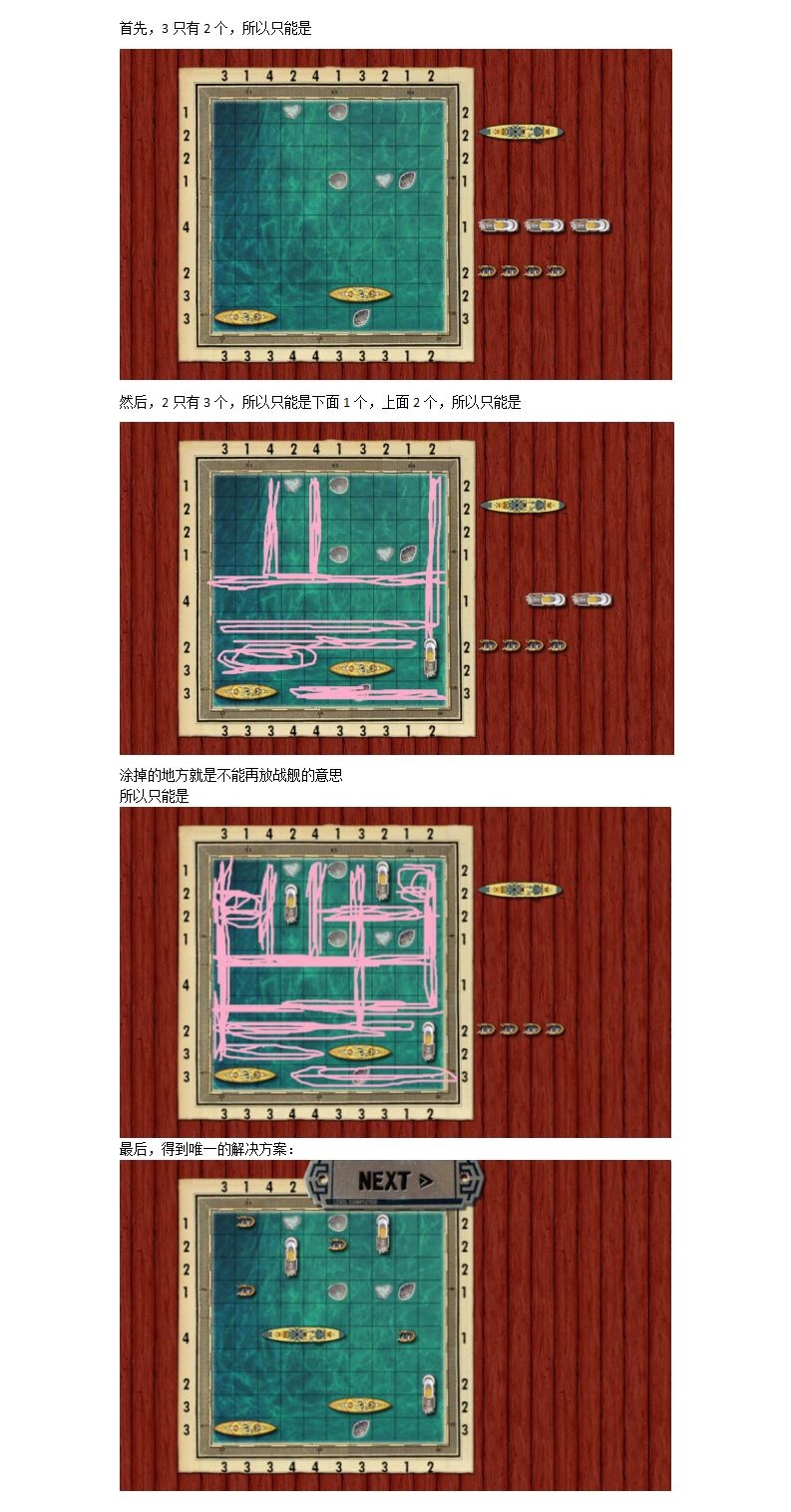
24 战舰(2)


这个游戏的规则,有些类似于

没错,这一关是有唯一解的。
69(5)
规则和上面一样。

107(8)
174(13)
先搞定长为 4 和 3 的这 3 个战舰,有唯一的位置。
然后再放下面 2 个长为 1 的战舰,这 2 个战舰都可以往上移一格,不过结果是一样的,对其他的战舰没有任何影响。

上面的部分,很容易就找到一个解了,没有深究是不是唯一解。

193(16)

211(19)

一共有 6 种方案,不过都差不多
227(22)
