大数据求topk问题

大数据求topk问题
大数据topk问题
1. 堆排序求topk

求上面序列中值最小的3个元素?
如果我们用排序来求解,选择基础排序算法(冒泡、选择、插入)达到O(n^2)的时间复杂度,选择高级排序算法(快排、归并、堆排)达到O(nlogn)。
但是如果要求在O(n)线性时间内找到top k的元素呢?
相当于是把原始序列遍历一遍就能找到top k个元素,实际上我们想一想,在这里面找值最大的或者值最小的前k个元素,也没有必要把所有元素都排序,因为其他的元素有没有序和我们关系不是很大。
在这里我们可以 用大小根堆解决top k问题
其实大小根堆是非常常用的,在互联网公司做产品,经常会有一些只能推荐,用户使用频率最高的一些应用或者是一些热点新闻、搜索频率最高的关键字等等,进行用户的推荐,在这里就需要对后台所存储的关键字、热点新闻,根据它查看次数或者搜索次数,进行top k的过滤,找到次数最大的前k个。
在这个问题里要求最小的前3个元素,需要用一个大根堆。

我们来演示一下,我们先遍历序列的前3个元素,把它构建成一个大根堆
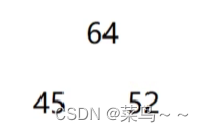
然后从第四个元素开始继续遍历,因为当前元素80和堆顶元素比较比堆顶元素大,这是一个大根堆,所以80就比堆顶所有元素都大,所以不用管80了,肯定不是最小的前3个元素,继续下一个元素,同样66、68也是比堆顶元素大,继续下一个元素,0比堆顶元素小,那么堆顶出堆,调整堆顶

继续下一个元素2

再看18、75

最终我们大根堆里面留下的这几个元素就是序列中值最小的前3个元素,时间复杂度为O(n),大根堆的调整和我们原始序列的数据规模没有关系,大小根堆调整的是树的层数O(logk),所以时间复杂度O(logk)*O(n),k是个常数所以时间复杂度为O(n)。

求最小的k个元素用大根堆:堆中加入小的淘汰大的
#include<iostream>
#include<vector>
#include<queue>
#include<time.h>
using namespace std;
int main()
{
vector<int> vec;
srand(time(0));
for (int i = 0; i < 1000; ++i)
{
vec.push_back(rand() % 1000 + 1);
}
//求vec中值最小的前5个元素
priority_queue<int> maxheap;
int k = 5;
//由前k个元素构成一个大根堆
for (int i = 0; i < 5; i++)
{
maxheap.push(vec[i]);
}
//遍历剩余的元素直到最后
for (int i = 5; i < vec.size(); ++i)
{
if (maxheap.top() > vec[i])
{
maxheap.pop();
maxheap.push(vec[i]);
}
}
//输出结果
while (!maxheap.empty())
{
cout << maxheap.top() << " ";
maxheap.pop();
}
}求最大的k个元素用小根堆:堆中加入大的淘汰小的
#include<iostream>
#include<vector>
#include<queue>
#include<time.h>
using namespace std;
int main()
{
vector<int> vec;
srand(time(0));
for (int i = 0; i < 1000; ++i)
{
vec.push_back(rand() % 1000 + 1);
}
priority_queue<int,vector<int>,greater<int>> minheap;
int k = 5;
for (int i = 0; i < 5; i++)
{
minheap.push(vec[i]);
}
for (int i = 5; i < vec.size(); ++i)
{
if (minheap.top() < vec[i])
{
minheap.pop();
minheap.push(vec[i]);
}
}
while (!minheap.empty())
{
cout << minheap.top() << " ";
minheap.pop();
}
}统计重复次数最小的前3个数字(使用优先级队列和哈希表)
#include<iostream>
#include<vector>
#include<queue>
#include<time.h>
#include<unordered_map>
#include<functional>
using namespace std;
int main()
{
vector<int> vec;
srand(time(0));
for (int i = 0; i < 1000; ++i)
{
vec.push_back(rand() % 100 + 1);
}
//统计重复次数最小的前三个数字
unordered_map<int, int> map;
for (auto key : vec)
{
map[key]++;
}
//放入大根堆的时候,需要放key-value键值对
using Type = pair<int, int>;
using Comp = function<bool(Type&, Type&)>;
priority_queue<Type, vector<Type>, Comp> maxheap(
[](Type& a, Type& b)->bool {
return a.second < b.second;
}
);
auto it = map.begin();
int k = 3;
for (int i = 0; i < k; i++)
{
maxheap.push(*it++);
}
for (; it != map.end(); ++it)
{
if (maxheap.top().second > it->second)
{
maxheap.pop();
maxheap.push(*it);
}
}
while (!maxheap.empty())
{
cout << "key:" << maxheap.top().first
<< " cnt:" << maxheap.top().second << endl;
maxheap.pop();
}
}2. 快排分割求topk
利用快排分割函数每次返回的基准数位置,找出前top k大的或者前top k小的数据。
#include<iostream>
using namespace std;
int Partition(int arr[], int l, int r)
{
int val = arr[l];
int i = l;
int j = r;
while (i < j)
{
while (i<j && arr[j]>val)
{
j--;
}
if (i < j)
{
arr[i] = arr[j];
i++;
}
while (i < j && arr[i] < val)
{
i++;
}
if (i < j)
{
arr[j] = arr[i];
j--;
}
}
arr[i] = val;
return i;
}
void SelectTopK(int arr[], int l, int r, int k)
{
int pos = Partition(arr, l, r);
if (pos == k - 1)
return;
else if (pos < k - 1)
{
return SelectTopK(arr, pos + 1, r, k);
}
else
{
return SelectTopK(arr, l, pos - 1, k);
}
}
int main()
{
int arr[] = { 34,23,12,67,87,56,90,0,19,14 };
int size = sizeof(arr) / sizeof(arr[0]);
int k = 3;
SelectTopK(arr, 0, size - 1, k);
for (int i = 0; i < k; i++)
{
cout << arr[i] << " ";
}
cout << endl;
return 0;
}最好时间复杂度:每次基准数都在中间,二叉树很平衡,n+n/2+n/4+1=O(n)
最坏时间复杂度:数据基本有序,基准数每次都在边上,二叉树退化为链表,O(n^2)