BP神经网络的数学表达式

[《老饼讲解神经网络》

“《老饼讲解神经网络》”)

目录

本文讲述BP神经网络在设定结构后，与之对应的数学表达式。

一. 模型结构

根据前面所述，BP神经网络的模型结构如下：

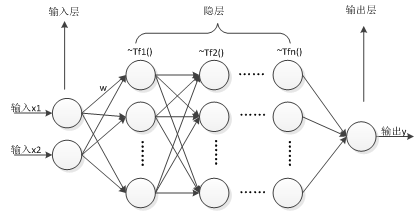
其中：

(1)  w： 是神经元与神经元之间的连接权重。

(2)  每个隐神经元与输出神经元都有各自的阈值b

(3) Tfi：每个神经元传递值之前，所作的转换函数 。即神经元的值在传递给其它神经元前，会先作Tfi()变换，然后再传递。

二. 模型结构设置

模型的隐层数目，传递函数，隐层节点个数都是由各具体问题具体设定，下面是一些常用的设置。

1.神经层数

输入输出层是必须的，其中隐层一般只设一个，因为有学者证明，一个隐层就能够逼近任何非线性函数。所以一般为：一个输入层，一个隐层，一个输出层。

下面的设置都假设只有一个隐层。

2. 隐层神经元个数

主要靠经验设置。一般先根据经验设置初始隐节点数，若果效果不好，再增加或减少一个试试，直到效果满意为止。

初始隐节点数的设置主要靠经验，下面给出一些实际经验作为参考：

(1) 一般5个以内的输入，使用3个隐节点就可以了，

(2) 有一次建模有20个输入变量，最后使用了7个隐节点。

3. 传递函数

输入层到隐层一般使用S型函数 tansig 作为传递函数，隐层到输出层一般则用purelin(线性)函数。

常用传递函数:

tansig  :

logsig  :

purelin :

三. 模型的数学表达式

假设我们最终的设置是：

1：一个输入层，一个隐层，一个输出层， 输入层、隐层、输出层的节点个数分别为 [2 ，3，1]。

2：传递函数设置：隐层（ tansig函数）。输出层（purelin函数）。

那么模型如下：

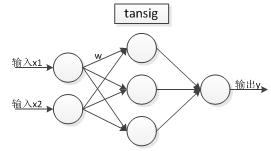
可以根据模型写出数学表达式如下：

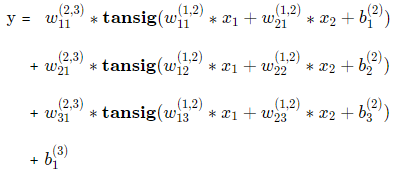
PASS: 表达式中参数很多，但实际只有两类参数：权重w和阈值b。

：代表这个权值是第2层的第1个节点到第3层的第1个节点的权值。

：代表这个阈值是第2层的第1个节点的阈值。

四.后语

在建好网络后，接下来就是使用历史数据训练网络（也即求解w,b的过程）。

通过训练，不断的调整网络的权重和阈值，使网络预测的输出与实际的输出误差尽量小。

请查看《 神经网络的训练方法 》

相关文章