算法导论-动态规划-最优二分检索树

目录
算法导论 · 动态规划 · 最优二分检索树
算法说明
构造最佳二叉搜索树:
如果已知集合元素的搜索概率,那么自然会提出一个关于最优二叉搜索树的问题,搜索中的平均比较数是可能的最小值。
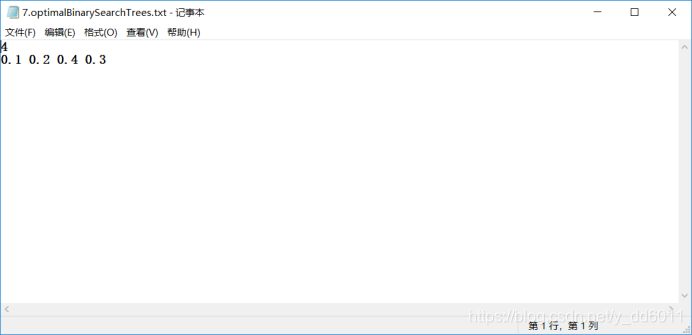
例如,考虑四个要搜索的键a、b、c和d,其概率分别为0.1、0.2、0.4和0.3。则0.1 1+0.2 2+0.4 3+0.3 4=2.9
源代码
#include <cstdio>
#include <cstring>
#define maxn 101
#define minc(a, b) (a) > (b) ? (b) : (a)
#define INF 1 << 29
double c[maxn][maxn], p[maxn];
int n, root[maxn][maxn];
int main() {
memset(c, 0, sizeof(c));
memset(root, 0, sizeof(root));
freopen("7.optimalBinarySearchTrees.txt", "r", stdin);
scanf("%d", &n);
for(int i = 1; i <= n; i++) {
scanf("%lf", &p[i]);
}
//init
for(int i = 0; i <= n; i++) {
c[i][i-1] = 0;
c[i][i] = p[i];
root[i][i] = i;
}
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n - k + 1; i++) {
int j = i + k - 1;
double sum = 0;
c[i][j] = INF;
for(int k = i; k <= j; k++) {
sum += p[k];
}
// printf("%d, %d, %.1f\n", i, j, sum);
for (int r = i; r <= j; r++) {
double t = c[i][r - 1] + c[r + 1][j] + sum;
if (c[i][j] > t) {
c[i][j] = t;
root[i][j] = r;
}
}
}
}
for(int i = 1; i <= n + 1; i++) {
for(int j = 0; j <= n; j++) {
if(c[i][j] == 0) printf("null ");
else printf("%-5.1f", c[i][j]);
}
printf("\n");
}
printf("\n");
for(int i = 1; i <= n + 1; i++) {
for(int j = 0; j <= n; j++) {
if(c[i][j] == 0) printf("null ");
else printf(" %-3d", root[i][j]);
}
printf("\n");
}
return 0;
}输入数据

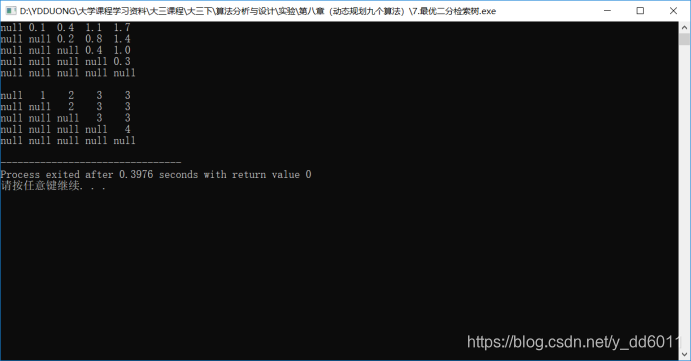
运行结果