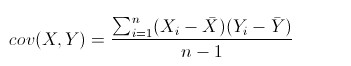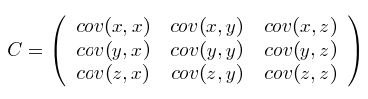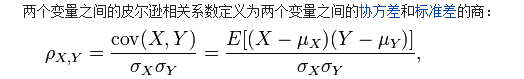数学名词的意义
数学名词的意义
前言：
最近在重学概率论，遇到很多名词、公式，感觉很高大上，只是因为看不懂！虽然可以通过练题去熟悉各个公式的使用，但我觉得此刻有必要对各种名词进行系统的总结，认识各种名词所代表的现实意义，和它们之间的关系，然后才能更深入地把概率论学好。
注：对于一个名词 最重要的有两点，做什么用？和怎么用？此处只以 通俗理解各名词的功用 为目的，不深究其用法，不追求数学严谨性。
数学期望：
设某人甲去赌钱，每次赌钱要40元，可以押Xi={20,40,60,100}四种选项（Xi对应赌赢可获得的钱额），各选项中的概率为Pi={0.5,0.3,0.15,0.05}：
则期望Eξ=20×0.5 + 40×0.3 + 60×0.15 + 100×0.05=36
即理论上 甲押上40元将得到36元。
所谓期望，其实也就是平均值，但是因为各个事件发生的概率不相等，所以不能像初中那样把所有数直接相加再除于n。
方差：var()
方差公式：
，其中x为平均值。
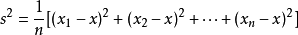
方差显示了数据集中各数据偏离平均值的程度，即数据离散的程度，或者叫波动的幅度。
标准差：
方差开根号即为标准差。它的作用和方差一样，也是显示数据的离散程度。
但我也不清楚既然标准差和方差联系这么近，作用又相同，为什么还要独立地定义这两个名词？
下面是摘自知乎上的一个回答，但我还是觉得独立定义两个名词的作用不是很明显。
协方差：cov()
前面的期望、方差都是用在一维数据上的，而协方差是用来表征二维数据中的相关关系的。
例如一个班上的数学成绩X和物理成绩Y组成的数据集，我们对它们求协方差，如果结果为正则表示两者有正相关关系，如果为负则表示负相关，若为0则表示两者不相关。
协方差公式：
协方差矩阵：
以上可以看到，协方差是表征二维数据、两个随机变量的相关性的。而对于多维的数据，就形成了协方差矩阵：
关于协方差和协方差矩阵请参考：
PS：网上转载了太多，已经不知道哪个才是原创，请原谅。
相关系数：
顾名思义，相关系数是用来表征变量之间的相关程度的。
相关系数用希腊数字γ表示，γ的范围为-1~1。γ>0为正相关，γ=0为不相关，γ<0为负相关。γ的绝对值越大，相关程度越高。而相关性的强弱并不是用绝对的数值来区分的，需要查具体的表：
变量之间的关系，并不是只用相关系数就可以确定的，还需要t检验、f检验等进行深入探究，这些以后再深入。更多相关系数的内容请参考 、
相关系数矩阵：
也称为相关矩阵，就像协方差到协方差矩阵那样，相关矩阵是由多维数据中多个相关系数构成的矩阵。
自由度：
我们需要n个数据一起，才能确定一个事物，则把n称为它的自由度。
例如在三维坐标系中的点，只要给出了x、y、z三个坐标，这个点就能确定下来，所以这个点的自由度就是3。
又例如在一个40人的班级里，已知数学成绩的平均分，只要知道任意39位同学的数学成绩，则剩下那位同学的成绩就只能是唯一的了，所以这里的自由度为df = n-1 = 40-1 = 39。
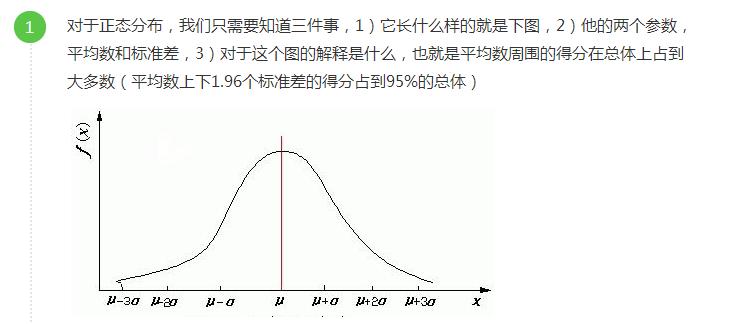
正态分布：
正态分布公式：
，μ是数学期望，σ²是方差。
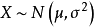
生活中大部分的事例都符合正态分布，大部分数据聚集在μ的周围，越靠近两边数据分布越稀疏。
更多关于正态分布的历史参见 、
t分布：
有关t分布、f分布、卡方分布请参见 、
f分布：
X ²分布：
exp：
