【离散数学】十章：图 - 图的表示和图的同构

📷10.4 图的表示和图的同构

图的表示方式有很多种，选择最方便的表示有助于对图的处理~

有时，两个图具有完全相同的形式，从某种意义上就是两个图的顶点之间存在着一 一对应，这个对应保持边的对应关系。在这种情形下，就说这两个图是 同构 的。

1. 图的表示

1.1 邻接表

表示不带多重边的图的一种方式是列出这个图的所有边。

另一种表示不带多重边的图的方式是邻接表，它给出了与图中每个顶点相邻的顶点。

注意，终点的个数 = 起点的出度数

1.1.1 简单图的邻接表

1.1.2 有向图的邻接表

1.2 邻接矩阵

假设图 G = (V, E) 是一个简单图，其中 |V| = n（ 顶点集元素的个数（顶点的个数）为n ） 假设把G 的顶点任意排列成 v 1 , v 2 , … , v n 。G 的邻接矩阵 A（或A G ） 是一个 n × n 的 0-1矩阵 ，它满足这样的性质：当 v i 和 v j 相邻时第( i, j )项是1，否则为0

若邻接矩阵是A G = [ a ij ]，则

**注意！

邻接矩阵外面是方括号“ [ ] ”，不可写成“ | | ”（这样就是行列式了）**

例题1：

用邻接矩阵表示图3所示的图。

🔴解：

把顶点排列成a, b, c, d，表示这个图的矩阵是：

例题2：

画出具有顶点顺序a，b，c，d的邻接矩阵的图

🔴解：

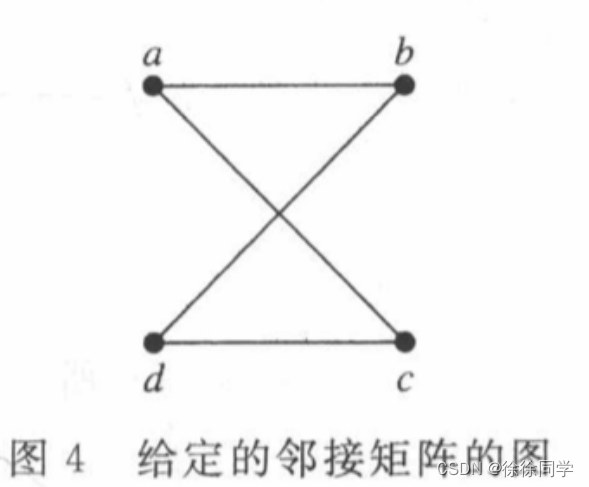
无向图 ⇒ 邻接矩阵对称

邻接矩阵对称 ⇏ 无向图

无向图的邻接矩阵一定是对称的，而有向图的邻接矩阵不一定对称

❗在邻接表和邻接矩阵之间取舍

当一个简单图包含的边相对较少，即该图是一个 稀疏图 时，通常 邻接表比邻接矩阵更适合表示它 。

需要注意的是，稀疏图的邻接矩阵是 稀疏矩阵 ，即矩阵中只有少量元素不为0。（有专门的技术表示和处理稀疏矩阵

👉 稀疏矩阵可以用邻接表，稠密矩阵可以用邻接矩阵表示

1.3 关联矩阵

表示图的另一种常用方式是用关联矩阵

设G = (V，E)是无向图。设 v 1 , v 2 , … , v n 是的图G的顶点，而e 1 ，e 2 ，…，e m 是该图的边。相对于V和E的这个顺序的关联矩阵是n×m的矩阵M=[m ij ]，

其中

任意一列有且仅有两个1（简单图）

每行" 1 “的个数 = 该行对应点的度

例题1：

用关联矩阵表示图6所示的图

🔴解：

例题2：

用关联矩阵表示图7所示的伪图：

🔴解：

2. 图同构

图的同构 类似于 “相似”

定义：简单图G 1 = (V 1 , E 1 ) 和 G 2 = (V 2 , E 2 ) 是简单图，若存在 一对一的 和 映上的 从 V 1 到 V 2 的函数 f ，且 f 具有这样的性质：对 V 1 中所有的a和b来说， a和b在 G 1 相邻当且仅当 f(a) 和 f (b) 在 G 2 中相邻，则称 G 1 和 G 2 是同构的。 这样的函数 f 称为同构

两个不同构的 简单图 称为非同构的

当两个简单图同构时，两个图的顶点之间具有保持相邻关系的一 一对应。所以， 图的同构是一个等价关系。

3. ⚡判断两个简单图是否同构

证明两个图不同构并不困难。如果能找到某个属性，两个图中只有一个图具有这个属性，但该属性应该在同构时保持，就可以说这两个图不同构。

这种在图的同构中保持的属性称为图形不变量。比如同构的简单图必须有相同顶点数、相同边数，对应顶点的度相同，邻接矩阵相同。

① 顶点个数、对应顶点的度、边数相等

② 回路中顶点个数相等

③ 图G中顶点w、v相邻 iff 在图H中 f(w) 、f(v)相邻

例题1：

判定图 G 和 H 是否同构。

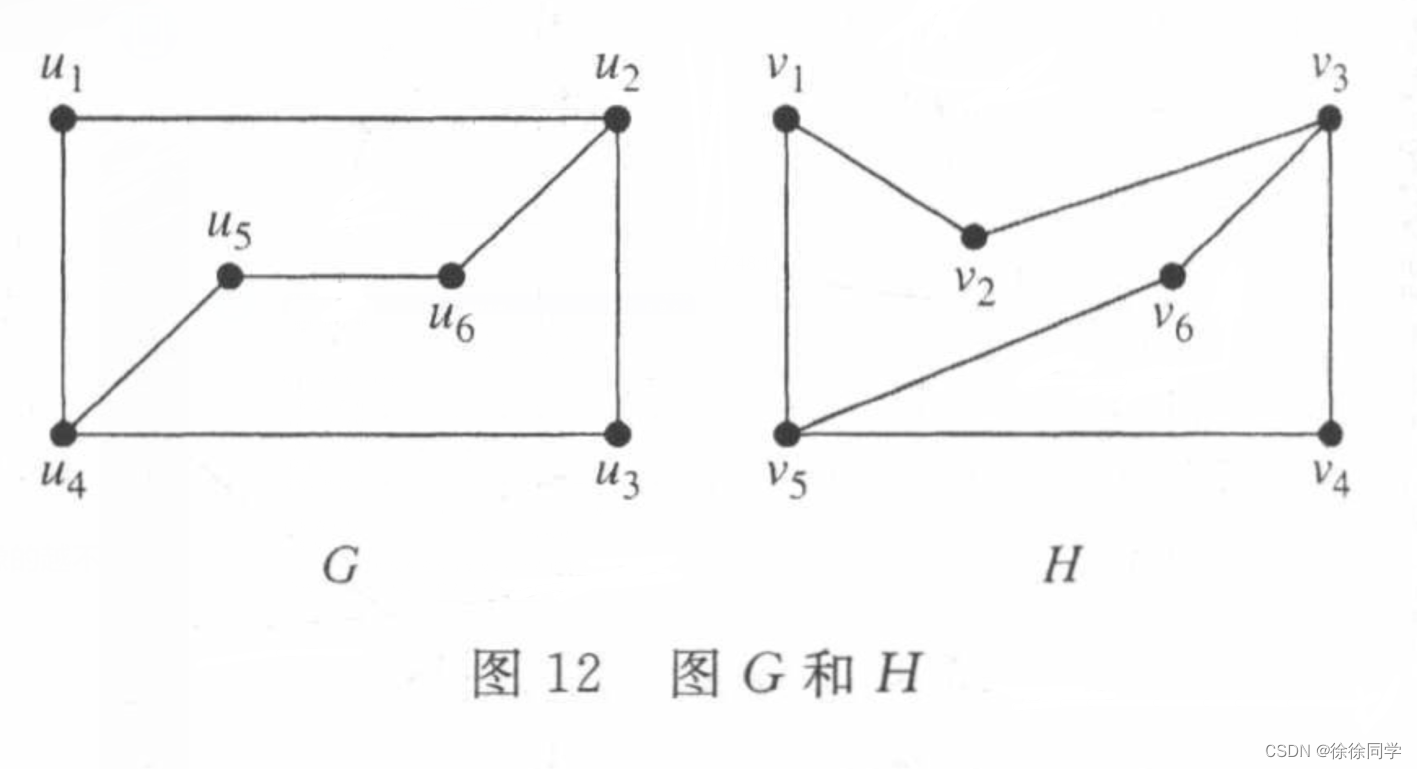
🔴解：

G的邻接矩阵：

H的邻接矩阵：

因为A G =A H ，所以 f 是同构的 → G 和 H 是同构的

！！！（ 考试时，越长得像的越不是同构 ）