技术博客
首页 所有文章 标签 分类 关于
技术博客

目录

数学建模优化模型规划模型

 收录于 未分类
   约 2846 字   预计阅读 6 分钟 
https://bing.ee123.net/img/rand?artid=135725981

【数学建模】优化模型——规划模型

在数学建模中，优化类问题是很常见的一种问题。这种问题里面通常涉及多个 变量 和 约束条件 ，并需要在这些变量和条件之下 优化某个函数 。最常见的例子就是，“达到最好效果”、“取得最大利润”、“极大降低风险”等等。遇到这类字眼，应首先考虑优化模型求解。

对于优化类模型，又细分为不同的算法来解决问题。常见的算法有： 规划模型 、 微分方程模型 、 图论网络优化 、 概率 、 智能优化算法 等。其中， 规划模型 是最基础的模型，是其他算法底层的根本原理，因此要想深入掌握其他模型，首先要学会规划模型。这篇文章就详细介绍一下规划模型。

https://i-blog.csdnimg.cn/blog_migrate/87b612961700e33f70a85716d2bb9794.png

目录

1 概述

1.1 什么是数学规划

数学规划是 运筹学 的一个分支，用来研究：在给定的条件（ 约束条件 ）下，如何按照某一衡量指标（ 目标函数 ）来寻求计划、管理、工作中的最优方案。通俗来讲就是： 求目标函数在一定约束条件下的极值问题 。

1.2 一般形式

m i n ( o r min(or

min

(

or

m a x ) max)

ma

x

)

z

f ( x ) z=f(x)

z

=

f

(

x

)

s . t . ( s u b j e c t s.t.(subject

s

.

t

.

(

s

u

bj

ec

t

t o ) to)

t

o

)

g i ( x ) ≤ 0 , i

1 , 2 , . . . g_i(x)≤0,i=1,2,…

g

i

​

(

x

)

≤

0

,

i

=

1

,

2

,

…

其中，

x x

x 为 决策变量 （一般多个），

f ( x ) f(x)

f

(

x

) 为 目标函数

这样的形式有些抽象，下面详细展开各类数学规划问题。

2 线性规划

**目标函数

f ( x ) f(x)

f

(

x

) 和约束条件均是决策变量的线性表达式** ——线性规划（Linear Programming）。

举个例子：

https://i-blog.csdnimg.cn/blog_migrate/e8bea7826f000a1a116ba264c930bd47.png

我们使用Matlab中的内置函数 linprog 来求解，底层实现原理为 单纯形法 ，不做过多展开。这里需要一定的线性代数基础，先来看一下函数原型：

[x, fval] = linprog(c, A, b, Aeq, beq, lb, ub, X0)

解释一下其参数：

  1. X0表示给定matlab迭代求解的初始值（一般不用给出）；
  2. c，A，b，Aeq，beq，lb，ub为 标准型 ，下面详细说明；
  3. 返回值x表示最小值处x的取值，fval表示最优解处取得的最小值；

标准型 ：

https://i-blog.csdnimg.cn/blog_migrate/8ff71a6f7c3662b94d82c6447d9e163a.png

注意事项 ：

  1. 若不存在 不等式约束 （即

    A X ≤ b AX≤b

    A

    X

    ≤

    b ）或 等式约束 （即

    A e q X

    b e q AeqX=beq

    A

    e

    qX

    =

    b

    e

    q ）可以用”[]“代替A、b、Aeq、beq；

  2. 若某个x无下界或上界，可以用-inf（无穷小）和inf（无穷大）来约束；

  3. 不是所有问题都有唯一解，可能 无解 或 有无穷多解 ；

  4. 如果求的是

    m a x max

    ma

    x ，可以先将目标函数 两侧取负号 化为标准型

    m i n min

    min ，再进行求解。

根据标准型，给出上面例子的matlab代码：

clear; clc
c = [-5 -4 -6]'; % '表示转置
A = [1, -1, 1
     3, 2, 4
     3, 2, 0];
b = [20 42 30]';
lb = [0 0 0]';
[x fval] = linprog(c, A, b, [], [], lb) % ub作为缺省参数，可以省略

运行即可得到结果：最小值fval为-78

3 非线性规划

顾名思义，目标函数和约束条件中存在非线性表达式。下面是一道例题：

https://i-blog.csdnimg.cn/blog_migrate/9995f6175173ace6bf9e787bf0fae13d.png

我们使用Matlab中的内置函数 fmincon 来求解。下面是函数原型：

[x, fval] = fmincon(@fun, X0, A, b, Aeq, beq, lb, ub, @nonlfun, option)

注意事项 ：

  1. 非线性规划中初始值X0的选取非常重要，因为其算法最终得到的是一个 局部最优解 ；

  2. 要求解全局最优解，建议使用 蒙特卡罗模拟 得到一个 蒙特卡罗解 ，然后用这个解作为初始值来求全局最优解；

  3. option 选项可以给定求解的算法，一共有四种：interior-point（内点法）；SQP（序列二次规划法）；active-set（有效集法）以及trust-region-reflective（信赖域反射算法），各有各的优点，建议都 都尝试一下 ；

  4. @fun表示目标函数，需要编写一个独立的文件来存储目标函数：

    function f = fun(X)
	% f = ...
end

  5. @nonlfun表示非线性约束部分，同样需要编写一个独立文件：

    function [C, Ceq] = nonlfun(X)
	% C = [非线性不等式约束1;
		   ...
		   非线性不等式约束n;]
	% Ceq = [非线性等式约束1;
		     ...
		     非线性等式约束m;]
end

标准型 ：

https://i-blog.csdnimg.cn/blog_migrate/b9cad45af1eb451a8177ca31e76b48d6.png

根据标准型，给出上面matlab代码：

% 文件fun.m
function f = fun(x)
    f = -x(1) ^ 2 - x(2) ^ 2 + x(1) * x(2) + 2 * x(1) + 5 * x(2);
end

% 文件 nonlfun.m
function [c, ceq] = nonlfun(x)
c = [(x(1) - 1) ^ 2 - x(2)];
ceq = []; % 不存在非线性等式约束
end

% 文件 main.m
clear; clc
format long g
x0 = [0, 0]; % 这里为了简便，随机给定一个初始值
A = [-2 3];
b = 6;
[x, fval] = fmincon(@fun, x0, A, b, [], [], [], [], @nonlfun)
fval = -fval

运行即可求解 fval 近似为-1。

改变求解算法的代码 ：

% 以内点法为例
option = optimoptions('fmincon','Algorithm','interior-point')

4 整数规划

整数规划 即为对数学规划加上 变量取值必须为整数 这一约束条件。其中，有线性整数规划和非线性整数规划两种问题。对于非线性整数规划，没有特定的算法来求解，只能使用近似算法（蒙特卡罗模拟、智能算法等），这里主要讲述线性整数规划。

对于 线性整数规划 ，我们使用 matlab 内置函数 intlinprog 进行求解。其函数原型为：

[x, fval] = intlinprog(c, intcon, A, b, Aeq, beq, lb, ub) % 新版还有初始值参数 X0，可以不指定

其参数含义和 linprog 类似，唯一不同的是 intcon 参数可以指定 哪些变量是整数 。

例如：

% x1, x2, x3 其中 x1,x3 是整数
intcon = [1, 3];

0-1 规划 即在整数规划的基础上， 变量取值只有 0 或 1 。典型例子为 0-1 背包问题，感兴趣的同学可以自行查阅相关题目。求解方法也很简单，只需要 **对约束变量的上下界设置为

[ 0 , 1 ] [0,1]

[

0

,

1

] 即可** 。

由于整数规划求解函数和线性规划非常类似，这里就不进行例题演示。

5 最大最小化模型

这个模型起源于对策论中，在最不利的环境下，寻求最有利的策略的问题。下面是这类问题的一般数学模型：

https://i-blog.csdnimg.cn/blog_migrate/f0d614fde2c77965571a15d259da5476.png

我们使用matlab中的内置函数 fminimax 来求解，下面是函数原型：

[x, fval] = fminimax(@Fun, X0, A, b, Aeq, beq, lb, ub, @nonlfun, option);

其函数参数和非线性规划函数 fmincon 类似，唯一不同的是第一个参数@Fun，代表目标函数

f 1 ( x ) , f 2 ( x ) , . . . , f m ( x ) f_1(x),f_2(x),…,f_m(x)

f

1

​

(

x

)

,

f

2

​

(

x

)

,

…

,

f

m

​

(

x

) ，其作为一个向量表示，代码操作如下：

function f = Fun(x)
    f = zeros(m, 1)
    % f(1) = ...
    % f(2) = ...
    % ...
    % f(m) = ,,,

end

6 多目标规划

顾名思义，即在一个规划问题中有 多个目标 。这种情况下，我们需要对多木雕进行 加权组合 ，把问题转化为单目标规划。举个例子：工厂生产时，既要考虑 利润 ，也要考虑 污染 。

注意事项

  1. 要将多个目标函数统一为 最大化或最小化 问题才可以进行加权组合
  2. 注意 量纲问题 ，多个函数由于量纲不同，不能直接加权。例如，污染指标和利润指标明显不是一个数量级。常用做法是： 用目标函数除以某一个常量，该常量是目标函数的一个取值，根据经验确定 。

【例题】

https://i-blog.csdnimg.cn/blog_migrate/f485582751c4ac63bac55a370acc2f0c.png

首先要对目标函数进行加权组合，这里我们假设权重分别为 0.4 和 0.6。用目标函数除以参考值以消除量纲：

f

0.4 × f 1 30 + 0.6 × f 2 2 f=0.4×\frac{f_1}{30}+0.6×\frac{f_2}{2}

f

=

0.4

×

30

f

1

​

​

0.6

×

2

f

2

​

​

然后就得到了一个单目标规划问题，根据上文的求解方法求解即可。

下面还有重要的一步就是 进行敏感性分析 。敏感性分析指的是 从定量分析的角度研究有关因素发生变化对某一个或一组关键指标影响程度的一种不确定分析技术 。说白了就是 改变相关变量的数值来解释关键指标受影响大小的规律 。

在这个问题中，我们需要改变

f 1 f_1

f

1

​

和

f 2 f_2

f

2

​

的权重，来观察对结果的影响。这里我们逐渐改变其权重，记录得到的

x 1 x_1

x

1

​

和

x 2 的值 x_2的值

x

2

​

的值 ，最终 得到的图像 （代码部分交给大家自己实现）：

https://i-blog.csdnimg.cn/blog_migrate/c04d466ce8b6c33c0a80e4aae95cf491.png

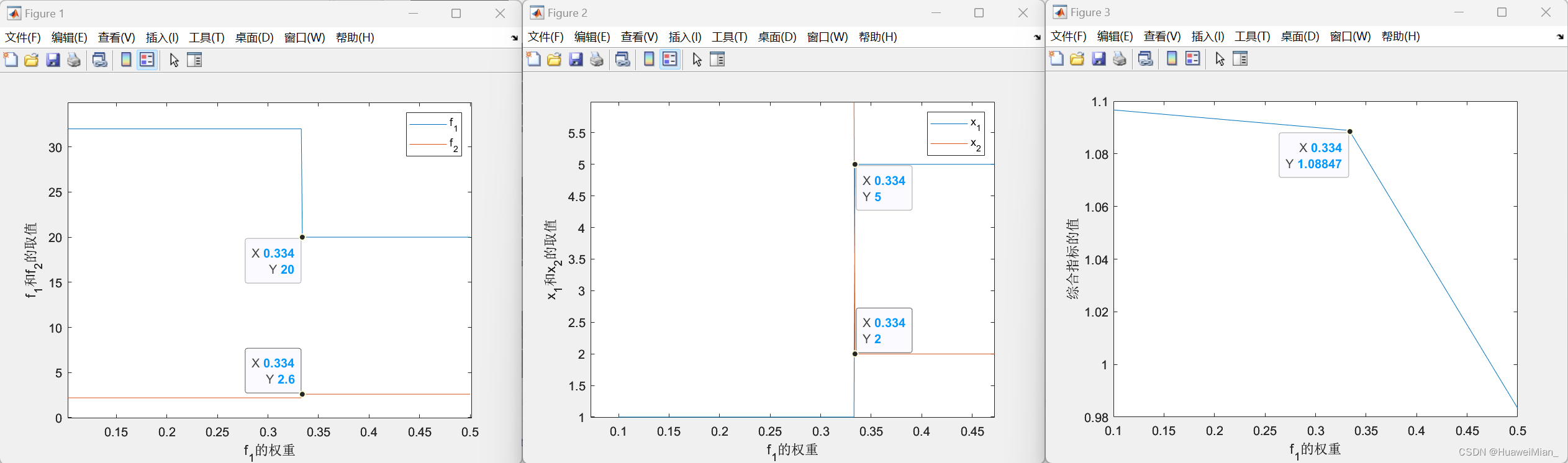
根据我们得到的结果，发现在0.333到0.334发生了突变，最后 结合实际问题做出解释 即可。

更新于 2024-01-21
 数学建模
返回 | 主页