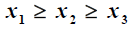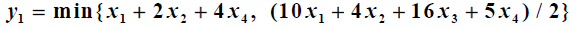【数学建模】下料问题

下料问题概述

下料问题生产中通过切割、剪裁、冲压等手段，将原材料加工成规定大小的成材.

优化问题按照工艺要求，确定下料方案，使所用材料最省，或利润最大.

钢管切割问题（一维）

题目1

如何下料最省？

分析

1、下料最省的标准（也就是最后的目标函数）

• 原料钢管剩余总余量最小;
• 所用原料钢管总根数最少.

2、由于采用不同切割模式太多, 会增加生产和管理成本,所以要规定切割模式不能超过几种，即切割模式自己设定为固定的几种。

3、按照客户需要在一根原料钢管上安排切割的某种排列组合，合理切割模式的余料应小于客户需要钢管的最小尺寸。

4、约束条件：

• 需求约束
• 原料约束
• 整数约束

求解

为满足客户需要，按照哪些种合理模式切割，每种模式切割多少根原料钢管，最为节省？

因此要设出来，最后找其中的约束关系，利用lingo求解。

思路1——总余量最少

解：设xi是 按第i种模式切割的原料钢管根数(i=1,…,7)

目标函数：

约束条件：

• 需求约束

  

• 整数约束

  xi均为整数

Lingo代码

model:
sets:
schema/1..7/:x,f;pipe/1..3/:b;link(pipe,schema):A;
endsets
data:
f=3,1,3,3,1,1,3;b=50,20,15;
A=4,3,2,1,1,0,0
0,1,0,2,1,3,0
0,0,1,0,1,1,2;
enddata
min=@sum(schema(i):(f(i)*x(i)));
@for(pipe(i):(@sum(schema(j):A(i,j)*x(j)))>=b(i));
@for(schema(i):@gin(x(i)));
end

思路2——总根数最少

解：设xi是 按第i种模式切割的原料钢管根数(i=1,…,7)

目标函数：

约束条件同上

题目2

增加1种需求：10根5m ；切割模式不超过3种；即现有4种需求：50根4m, 10根5m, 20根6m,15根8m；

若用枚举法确定合理切割模式，过于复杂。因此， 对大规模问题, 用模型的约束条件界定合理模式。（直接设）设出每一种模式的切割方式，及按照每种模式切割的数量。但是注意，模式不要设置太多，可以自己固定模式数量的上限，否则不仅自己求解困难，在实际生产中管理也过为复杂。

求解

解:设xi是按第i 种模式切割的原料钢管根数(i=1,2,3);

r1i, r2i, r3i, r4i是第i 种切割模式下, 每根原料钢管生产4m、5m、6m和8m长的钢管的数量.

目标函数：（总根数最少）min=x1+x2+x3;

约束条件：

• 需求约束

  

• 原料约束（切割模式合理）

  

• 缩小可行域约束（根据第一问的规律得出）

  

• 整数约束

  xi,rij均为整数

Lingo代码

model:
sets:
schema/1..3/:x;pipe/1..4/:b,c;link(pipe,schema):r;
endsets
data:
b=50,10,20,15;c=4,5,6,8;
enddata
min=@sum(schema(i):x(i));
@for(pipe(i):(@sum(schema(j):r(i,j)*x(j)))>=b(i));
@for(schema(j):(@sum(pipe(i):r(i,j)*c(i)))<19);
@for(schema(j):(@sum(pipe(i):r(i,j)*c(i)))>=16);
@for(schema(i):@gin(x(i)));
@for(schema(j):@for(pipe(i):@gin(r(i,j))));
x(1)>=x(2);
x(2)>=x(3);
end

易拉罐下料（二维）

分析

目标:易拉罐利润扣除原料余料损失后的净利润最大

注意:不能装配的罐身、上下底也是余料

约束：工作时间；原料数量；配套组装

求解

解：设决策变量如下：

xi ~ 按照第i 种模式的生产张数(i=1,2,3,4)；

y1 ~ 一周生产的易拉罐个数；

y2 ~ 不配套的罐身个数；

y3 ~ 不配套的底、盖个数.

每只易拉罐利润0.10元，余料损失0.001元/ cm2，罐身面积PI d h=157.1 cm2；底盖面积PI d d/4=19.6 cm2

目标函数：

max=0.1 y1-0.001 (222.6 x1+183.3 x2+261.8 x3+169.5 y2)

约束：

• 时间约束

  

• 原料约束

  

• 配套约束

  

  

  

总结

一维问题若模式不多，可枚举出来，则列举出所有情况，设出采用每种模式切割的个数，找到合适的约束条件，建立整数线性规划模型。

若模式枚举不过来，则 构造整数非线性规划模型, 将各种模式设出来（每种模式如何切割），同时设出采用每种模式切割的数量 ，然后多找约束条件（如：满足需求、切割模式合理等），列出多个不等式。 可用缩小可行域的方法进行化简, 但要保证最优解的存在。

二维、三维问题类似。

切割模式相关软件

CutMaster

CutLogic 2D

附三维问题：

快递包装问题

某企业为下游快递公司生产包装纸箱。该企业生产的原始瓦楞纸有四种型号，皆为正方形，其边长分别为2.5m，2.0m，1.8m, 1.5m, 三层瓦楞板成本分别为10.0，6.5，4.8，4.0元。瓦楞纸边角料可以以每平米1.4元在其企业内部回收利用。五层瓦楞板成本为对应三层板的1.3倍。

问题1.　请利用下表中的数据给出合理的假设，确定该企业1天的生产计划，使其利润最大。

问题2.　如果实际中，提供给下游快递公司的纸箱在容积误差30%之内可以以大纸箱代替小纸箱供货，那么新的最优生产计划是什么？

问题3.　哪一种快递纸箱的需求变化对生产计划最为敏感？

可以展开如下图后参照二维模型进行求解