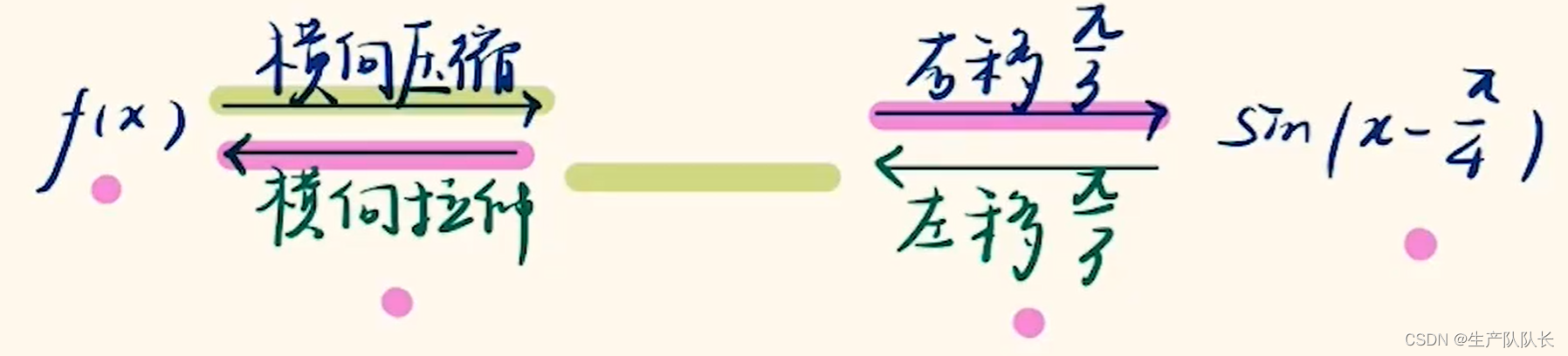高中数学：三角函数-函数的平移伸缩及一般形式

一、基本平移

左加右减，上加下减

二、伸缩

1、横向伸缩（频率）

2、纵向伸缩（振幅）

3、平移与伸缩的顺序

会发现，顺序不同，平移的量不一样

4、例题

说明：

左加右减和横向伸缩，都是针对自变量 x 的变化

上加下减和纵向伸缩，都是针对函数值 y 的变化

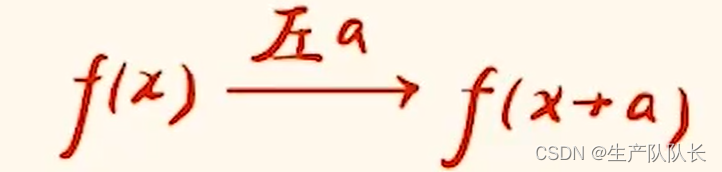
三、一般形式

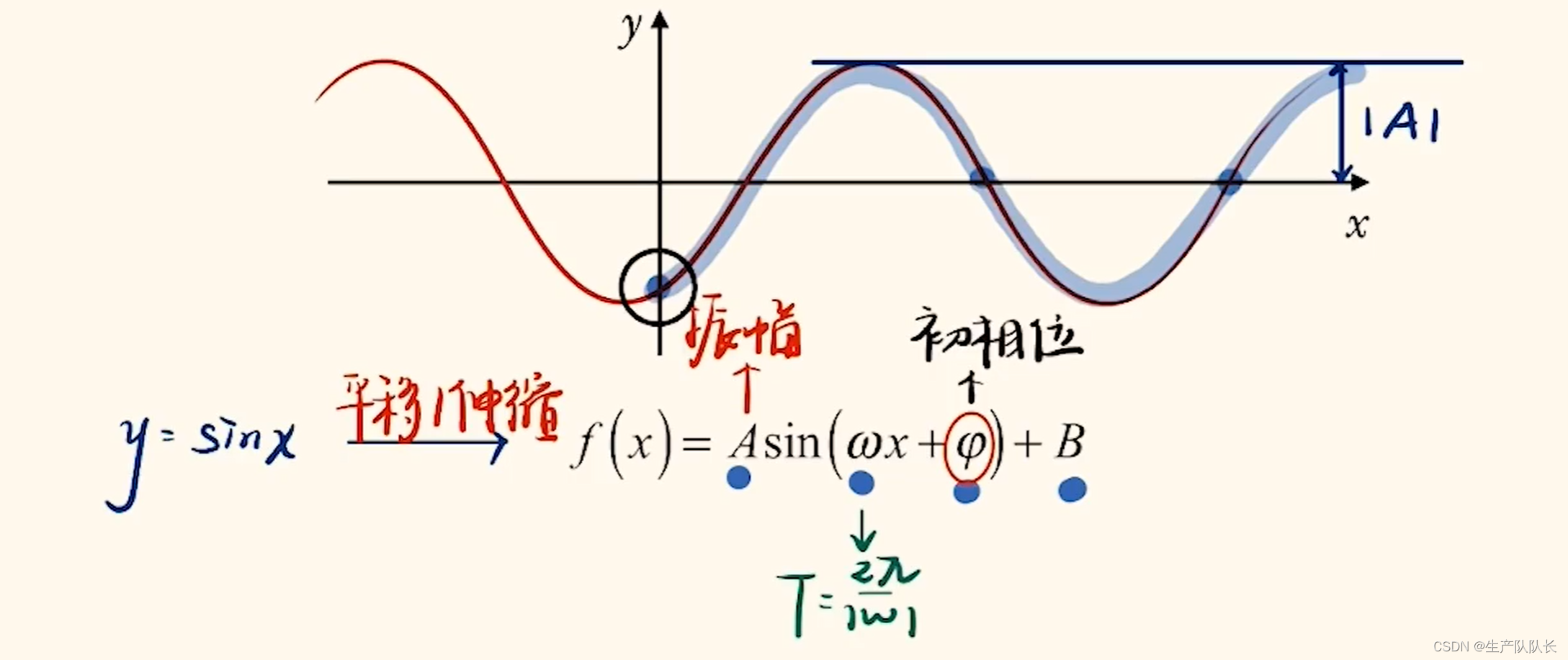
各参数说明：

A：影响图像的振幅，即函数的值域范围

ω：影响函数周期

φ（重点） ：决定函数的初相位，即图像与y轴的交点

B：对函数图像整体上下平移

建议的画图顺序：

f(x) -> Af(ωx) -> Af(ωx+φ)+B

四、练习

例题1

解析：

左加右减是针对自变量x的计算

例题2

解析：

先用诱导公式，将cosx变化为sinx，然后，进行平移伸缩即可

例题3

解析：

逆向思维