CSP数学专题

目录 ：

三角函数

数学逻辑运算

流程图的概念

同余定理

组合排列

三角函数

正弦函数（sin）

余弦函数（cos）

正切函数 （tan）

常见特殊角度的三角函数值

对数函数是数学中的一类常见函数，以对数为基础定义

自然对数函数 :

自然对数函数用符号“In”表示，以常数e(自然对数的底)为底的对数函数。

1n(x)表示x的自然对数，其中x是正实数。

通用对数函数 :

通用对数函数用符号“log”表示，以常数10为底的对数函数

log(x)表示x的通用对数，其中x是正实数

对数的性质 :

对数函数的定义域是正实数集，值域是实数集。

对数函数的图像呈现递增曲线，且在x=1处有一个垂直渐近线。

对数函数1n(x)的特殊值 In(1)=0，即 In(e) = 1

对数函数 log(x)的特殊值 log(1) = 0，即 log(10) = 1

2.数学逻辑运算

数学逻辑运算是研究命题之间关系的数学分支

逻辑与 :用符号"∧ ”表示，表示两个命题同时为真时整个逻辑表达式为真

逻辑或 :用符号"∨ ”表示，表示两个命题至少有一个为真时整个逻辑表达式为真

逻辑非 :用符号"⇁ ”表示，表示对一个命题的否定

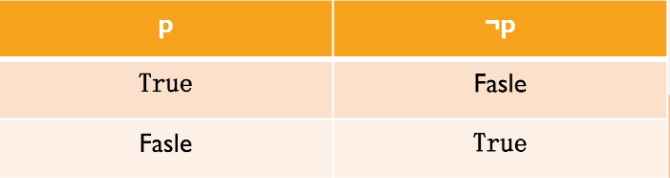
逻辑蕴含 :用符号"→”表示，表示若前提为真，则结逻辑蕴含论为真

3.集合

集合，简称集，是数学中一个基本概念，其定义为:由一个或多个确定的元素所构成的整体。集合内的元素不会有重复，例如:

结论 :

1.集合的“并”运算对应于常见数学逻辑用语中的“或”，所以二者的符号也比较相像 (并:U，或:V)，开口方向都向上。

2.集合的“交”运算对应于常见数学逻辑用语中的“且”运算，二者的符号比较相像（交:n，且:∧)，开口方向都向下。

4.流程图的感念

算法的表示方法

伪代码是用介于自然语言和计算机语言之间的文字和符号(包括数学符号)来描述算法。

书写规则 :

Begin作为开始，End作为结束

Begin

输入 A,B

IF A>B

End

Print A

伪代码的语法规则

在伪代码中，每一条指令占一行(elseif，例外)。指令后不跟任何符号(Pasca1和C中语句要以分号结尾)

变量

算法中出现的数组、变量可以是以下类型:整数、实数、字符、位串或指针。通常这些类型可以从算法的上下文来看是清楚的，并不需要额外加以说明比如:整型(1，2，166)，浮点型(1.23,3.1415)，字符串(“helloworld”),字符(A，F)，布尔型(True,False)

表达式符号

+，-，*，/，~，<=,>，and,or,not

输入输出

Input:输入0utput:输出Read:

读取输入

Print:打印输出

return:算法执行的终点,返回

赋值

赋值语句用符号“<—–”表示<变量>=<表达式)

例子:

X<—-y 将Y的值赋给X

伪代码的语法规则

在伪代码中，每一条指令占一行(else if，例外)

4.同余定理

数学上，两个整数除以同一个整数，若得相同余数，则二整数同余

例如:

1/3 =0 …1

4/3=1…1

则1和4对模3同余

记作1 ≡ 4(mod 3)

读作:1同余于4模3，或读作1与4对模3同余

同余定理的作用 :

同余定理可用于快速计算大数的幂运算

同余定理在密码学中起着重要的作用两个大质数p和q用于生成公钥和私钥，其中公钥包含指数和模数私钥包含指数和模数的因子。同余定理用于加密和解密过程中对模幂运算的处理，确保加密和解密操作的正确性

4.排列组合

组合

组合是从给定的对象中选择若干个对象按照任意顺序组成的方式组合只考虑对象的选择，不考虑其顺序和位置

组合的结果不受选择对象的顺序和位置的影响

从n个不同元素中取出m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数

从8个人中选择4个人组成一个小组，共有多少种不同的组合方式

组合用符号A

排列组合的区别

排列的应用场景:当我们关心对象的顺序和位置时，使用排列。例如，考虑队伍中不同位置的排列顺序、选择固定位置的对象等

组合的应用场景:当我们只关心对象的选择而不考虑其顺序和位置时，使用组合。例如，从一组人员中选择小组成员、从一组元素中选择子集等

制作不易，点赞

从我的信奥OJ上搬来的