2024年中国研究生数学建模竞赛C题“数据驱动下磁性元件的磁芯损耗建模”全析全解

↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑

总领这个题，是属于数据挖掘和数据优化类型的题目，对于数据的要求非常高，数据的精确度和有效性能够直接决定磁心损耗的评价的准确度，所以在进行问题的建模时，首先需要对数据进行数据预处理。

数据预处理的步骤为：数据清洗、数据归一化等等。

数据清洗是数据处理中的重要环节，由于数据源头不一，直接导致数据质量参差不齐，因此必须要做好数据清洗。

去重：移除重复的样本，确保数据多样性

去噪：过滤掉无意义的数据，如广告，拼写错误，噪声图像等

统一格式：确保所有数据采用一致的编码格式(如UTF-8)，并且统一时间，日前等标准格式；

数据修复：修正数据中的错误，如拼写，补全等。

数据归一化的方法：

数据归一化是数据预处理中的一个重要步骤，它对于提高机器学习模型的性能、加速训练过程以及改善数据分布特性具有重要意义。以下是关于数据归一化的意义和方法的详细解答：

数据归一化的意义

1. 消除尺度差异：不同特征可能具有不同的尺度和范围，这可能导致某些特征在模型训练中起主导作用，而其他特征的影响被忽略。归一化可以消除特征之间的尺度差异，确保每个特征对模型的贡献相对平等。
2. 加速模型收敛：在训练深度神经网络等模型时，数据的归一化可以加速模型的收敛。这是因为在归一化后，模型的参数更新更加稳定，训练过程更容易找到损失函数的最优解。
3. 提高模型精度：对于某些算法，如K近邻算法（KNN）和神经网络，特征的尺度对模型的性能有显著影响。归一化可以帮助这些算法更准确地捕捉特征之间的关系，从而提高模型的精度。
4. 防止数值问题：在某些计算过程中，如使用梯度下降算法时，如果特征的尺度差异很大，可能会导致数值不稳定或梯度消失/爆炸的问题。归一化有助于避免这类数值问题。
5. 提高模型稳定性：归一化可以提高算法的稳定性，使得算法对于不同的数据集或数据子集具有更一致的性能。

数据归一化的方法

数据归一化有多种方法，以下是几种常用的方法：

1. Min-Max归一化（最小-最大规范化）—-常用

• 方法描述：也称为线性归一化，通过将数据缩放到[0, 1]区间内，实现数据的归一化。
• 公式：

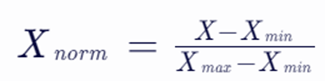
• 其中，X 是原始数据，Xmin​ 和 Xmax​ 分别是数据集中的最小值和最大值，Xnorm​ 是归一化后的数据。
• 优点：简单直观，易于实现。
• 缺点：对极端值非常敏感，如果数据集中存在离群值，可能会影响归一化效果。

1. Z-Score归一化（标准化）—（本文推荐应用）

• 方法描述：将数据转换为均值为0，标准差为1的正态分布（也称为标准正态分布或高斯分布）。
• 公式：

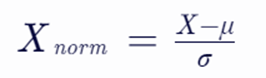
其中，X 是原始数据，μ 是原始数据的均值，σ 是原始数据的标准差，Xnorm​ 是标准化后的数据。

• 优点：不受离群值影响，适用于数据分布接近正态分布的情况。
• 缺点：对于非正态分布的数据，可能不是最佳选择。

1. 小数定标规范化

• 方法描述：通过移动特征数据的小数位数，将其转换到特定区间内，如[-1, 1]。
• 公式：根据特征值绝对值的最大值决定移动的小数位数。
• 优点：适用于不同量级的数据，可以通过调整小数位数来适应不同的区间需求。
• 缺点：需要手动确定小数位数，且对于极端值可能不太敏感。

1. 非线性归一化方法

• 方法描述：包括对数变换、平方根变换、指数变换等，通过非线性函数将数据映射到新的区间内。
• 优点：能够改善数据的分布特性，特别是对于偏态分布的数据。
• 缺点：需要根据数据的具体分布选择合适的非线性函数。

在选择归一化方法时，需要根据数据的特性和后续算法的需求进行综合考虑。例如，在分类、聚类算法中，如果需要使用距离来度量相似性，或者使用PCA技术进行降维时，Z-Score归一化表现可能更好。而在不涉及距离度量、协方差计算、数据不符合正态分布的情况下，可以使用Min-Max归一化或其他归一化方法。

数据预处理完后，就根据问题对下列问题的分析

问题一：励磁波形分类

思路：

1. 数据准备：读取附件一中的磁通密度数据。

2. 特征提取：分析磁通密度的分布特征及不同波形的形状特征，提取出反映磁通密度分布及波形的形状特征变量。

3. 分类模型建立：利用提取的特征变量建立分类模型，识别出励磁的三种波形（正弦波、三角波和梯形波）。

4. 模型验证：使用附件二中的样本数据验证分类模型的合理性及有效性。

5. 结果填入表格：将分类结果填入附件四（Excel表格）中第2列，并统计出三种波形的各自数量。

数学建模过程：

• 特征提取：可以通过计算磁通密度的时间导数和加速度等特征来描述波形的形状。

• 分类算法：可以使用支持向量机（SVM）、随机森林（Random Forest）或K近邻（KNN）等分类算法。

问题二：斯坦麦茨方程（Steinmetz-equation）修正

思路：

1. 数据分析：分析斯坦麦茨方程在不同温度变化下的磁芯损耗预测效果。

2. 模型修正：构造一种可适用于不同温度变化的磁芯损耗修正方程。

3. 效果比较：比较修正方程与斯坦麦茨方程的预测效果。

数学建模过程：

• 修正方程：在原斯坦麦茨方程基础上，增加温度因素，构造修正方程。

• 效果评估：使用均方误差（MSE）或平均绝对误差（MAE）等指标评估两个模型的预测效果。

………………………………………………………………………………

↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓