2024-10-28-南京邮电大学数学实验模块四种群增长模型与综合实验参考答案

南京邮电大学《数学实验》模块四(种群增长模型与综合实验)参考答案
4.1

代码如下:
i=0;
m=[];
n=1000;
for a=1:n
for c=a+1:n
b=sqrt(c^2-a^2);
if(b==floor(b))&(c==b+2)
i=i+1;m(:,i)=[a,b,c];
end
end
end
m测试结果如下:

表示公式为:
{a,b,c}={(2u)^2,(u^2-1)^2,(u^2+1)^2}
4.2
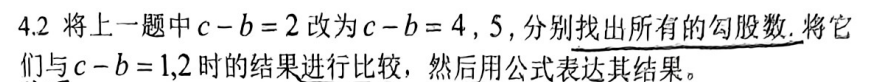
测试结果如下:
(1)c==b+4时,
代码如下:
i=0;
m=[];
n=1000;
for a=1:n
for c=a+1:n
b=sqrt(c^2-a^2);
if(b==floor(b))&(c==b+4)
i=i+1;m(:,i)=[a,b,c];
end
end
end
m测试结果如下:
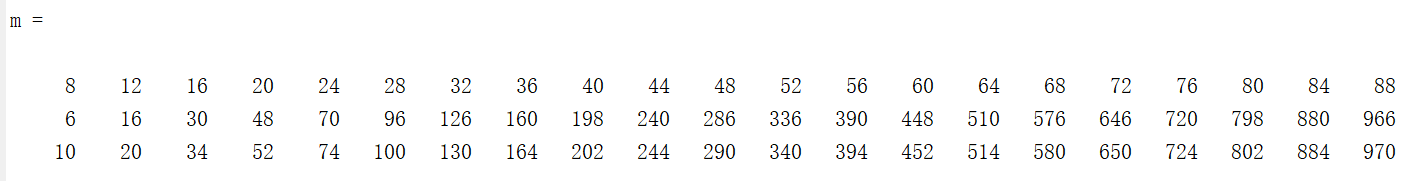
表示公式为:
{a,b,c}={(4u)^2,(2u^2-2)^2,(2u^2+2)^2}
(2)c==b+5时,
代码如下:
i=0;
m=[];
n=1000;
for a=1:n
for c=a+1:n
b=sqrt(c^2-a^2);
if(b==floor(b))&(c==b+5)
i=i+1;m(:,i)=[a,b,c];
end
end
end
m测试结果如下:
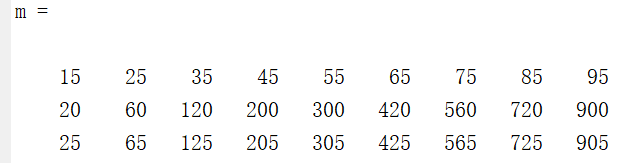
表示公式为:
{a,b,c}={(5u)^2,((5u^2-5)/2)^2,((5u^2+5)/2)^2}
4.3

代码如下:
for k=1:200
for b=1:999
a=sqrt((b+k)^2-b^2);
if((a==floor(a))&&gcd(gcd(a,b),(b+k))==1)
fprintf('%i,',k)
break;
end
end
end测试结果如下:
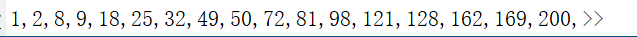
特征:满足条件的K值为完全平方数或完全平方数的平方。
预测结果:225,242,288,289共四个数。
4.4

代码如下:
d0=9;
x=[1.5,1.8,2.4,2.8,3.4,3.7,4.2,4.7,5.3];
y=[8.9,10.1,12.4,14.3,16.2,17.8,19.6,22.0,24.1];
d1=sum(x);
d2=sum(x.^2);
b1=sum(y);
b2=sum(y.*x);
A=[d0,d1;d1,d2];
B=[b1;b2];
u=A\B;
a0=u(1)
a1=u(2)
error=sum((y-(a0+a1.*x)).^2)测试结果如下:

即所求方程为:y=2.8304+4.0244x
误差为0.2409
4.5

(1)代码如下:
t=1790:10:1980
x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5];
t1=t(1);
x1=x(1);
t2=t(16);
x2=x(16);
A=[1,t1;1,t2];
B=[log(x1);log(x2)];
u=A\B;
x0=exp(u(1))
k=u(2)
error=sum((x0*exp(k*t)-x).^2)测试结果如下:

所得x0、k、error即为所求。
(2)代码如下:
t=1790:10:1940
%不同学号对应的数据可能不同,请仔细审题
x=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7];
y=log(x);
m=length(t);
A=[m,sum(t);sum(t),sum(t.^2)];
B=[sum(y);y*t'];
u=A\B;
x0=exp(u(1))
k=u(2)
error=sum((x0*exp(k*t)-x).^2)测试结果如下:
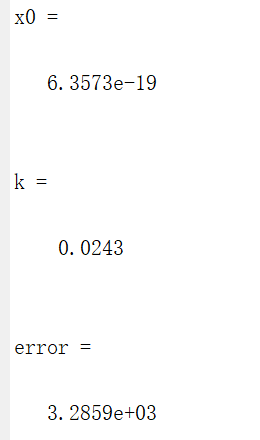
所得x0、k、error即为所求。
4.6

代码如下:
x=1:26;
y=[1807,2001,2158,2305,2422,2601,2753,2914,3106,3303,3460,3638,3799,3971,4125,4280,4409,4560,4698,4805,4884,4948,5013,5086,5124,5163];
a=[6000,2,0.1];
f=@(a,x)a(1)./(1+a(2)*exp(-a(3)*x));
[A,resnorm]=lsqcurvefit(f,a,x,y)
t=26;
while abs(A(1)/(1+A(2)*exp(-A(3)*t))-A(1)/(1+A(2)*exp(-A(3)*(t+1))))>1
t=t+1;
end
t
s=f(A,t)
i=1:t;
plot(x,y,'*')
hold on;
plot(i,A(1)./(1+A(2)*exp(-A(3)*i)));
grid on
legend('原始数据','拟合曲线','Location','SouthEast')测试结果如下:
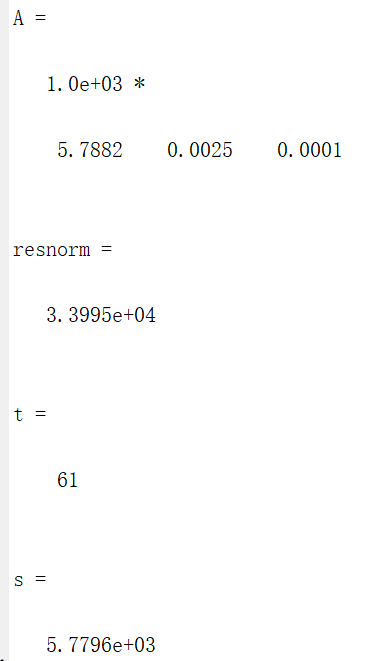
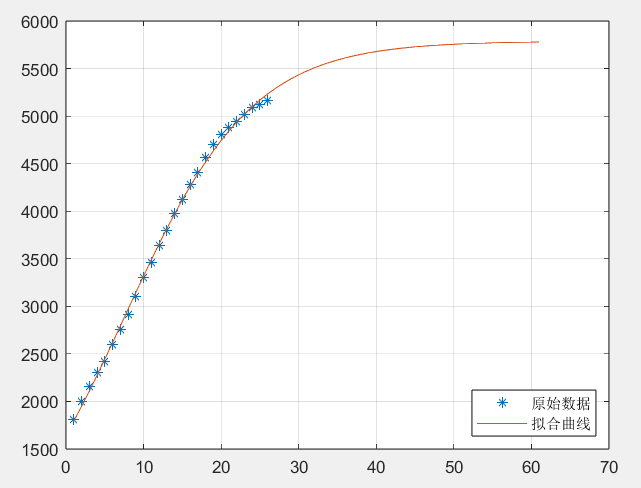
即最终规模人数达5788人,预计历时61天,在6月19日疫情结束。
4.7

代码如下:
x=1:26;
y=[1807,2001,2158,2305,2422,2601,2753,2914,3106,3303,3460,3638,3799,3971,4125,4280,4409,4560,4698,4805,4884,4948,5013,5086,5124,5163];
a=[6000,2,0.1,0.1];
f=@(a,x)a(1)./(1+a(2)*exp(-a(3)*x-a(4)*x.^2));
[A,resnorm]=lsqcurvefit(f,a,x,y)
t=26;
while f(A,t+1)-f(A,t)>=1
t=t+1;
end
t
s=f(A,t)
%
i=1:t;
plot(x,y,'*')
hold on;
plot(i,A(1)./(1+A(2)*exp(-A(3)*i-A(4)*i.^2)));
grid on
legend('原始数据','拟合曲线','Location','SouthEast')测试结果如下:
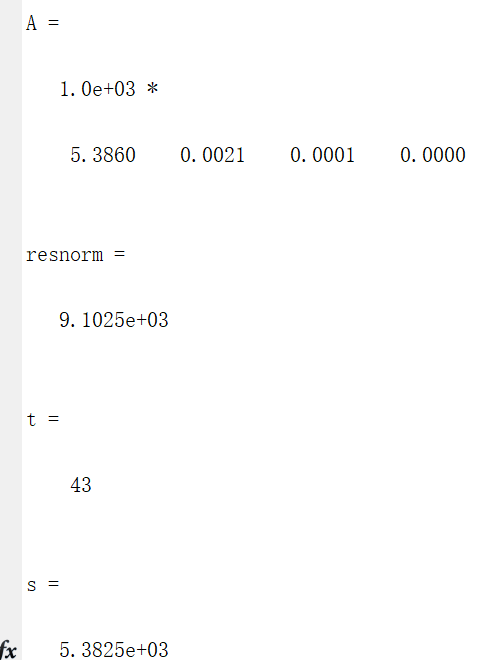
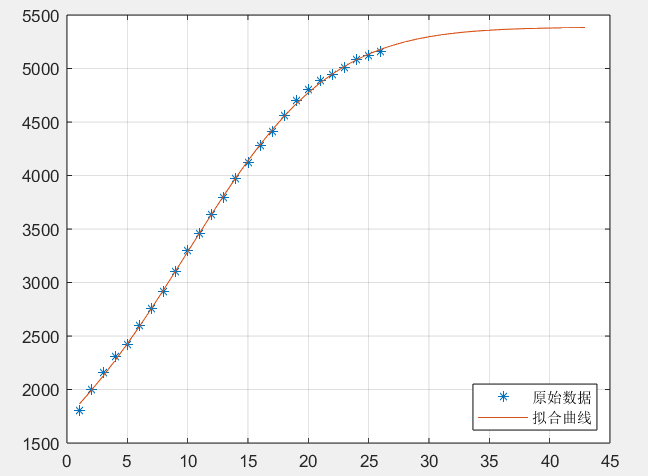
即最终规模人数达5383人,预计历时43天,在6月1日疫情结束。
4.8

代码如下:
x=1:27;
y=[21,65,127,281,558,923,1321,1801,2420,3125,3886,4638,5306,6028,6916,7646,8353,9049,9593,10098,10540,10910,11287,11598,11865,12086,12251];
a=[10000,2,0.1];
f=@(a,x)a(1)./(1+a(2)*exp(-a(3)*x));
[A,resnorm]=lsqcurvefit(f,a,x,y)
t=27;
while abs(A(1)/(1+A(2)*exp(-A(3)*t))-A(1)/(1+A(2)*exp(-A(3)*(t+1))))>1
t=t+1;
end
t
A(1)/(1+A(2)*exp(-A(3)*(t+1)))
i=1:t;
plot(x,y,'*')
hold on;
plot(i,A(1)./(1+A(2)*exp(-A(3)*i)));
grid on
legend('原始数据','拟合曲线','Location','SouthEast')测试结果如下:
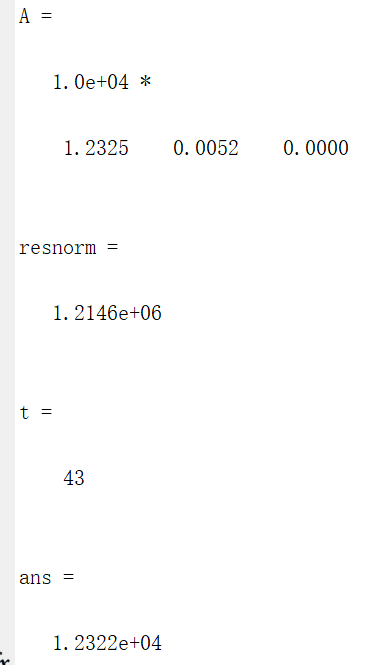
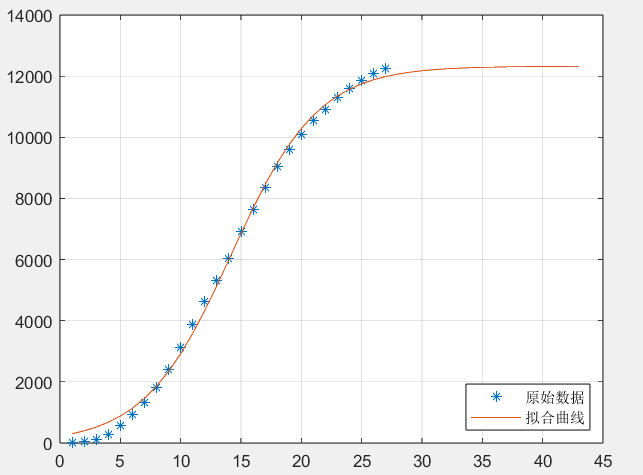
变化函数为x(t)=12325/(1+52.386*e^(-0.2879t)),最终规模人数达12322人,预计历时43天,在3月2日疫情结束。
4.9
代码如下:
x=1:27;
y=[21,65,127,281,558,923,1321,1801,2420,3125,3886,4638,5306,6028,6916,7646,8353,9049,9593,10098,10540,10910,11287,11598,11865,12086,12251];
a=[4,0.1,0.1];
f=@(a,x)a(1)*exp(exp(a(2)*x+a(3)));
[A,resnorm]=lsqcurvefit(f,a,x,y)
t=27;
while abs(f(A,t)-f(A,t+1))>1
t=t+1;
end
t
f(A,t+1)
t=1:50;
plot(x,y,'*')
hold on;
plot(t,f(A,t));
grid on
legend('原始数据','拟合曲线','Location','NorthWest')测试结果如下:
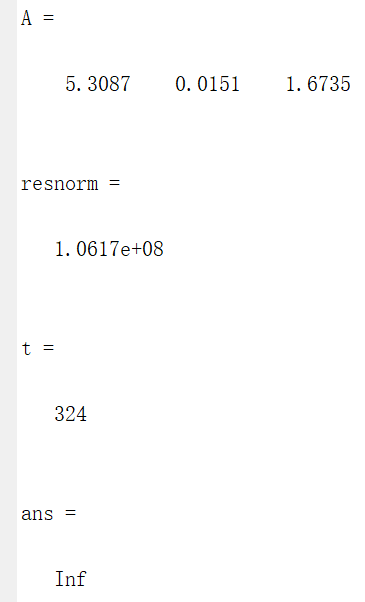
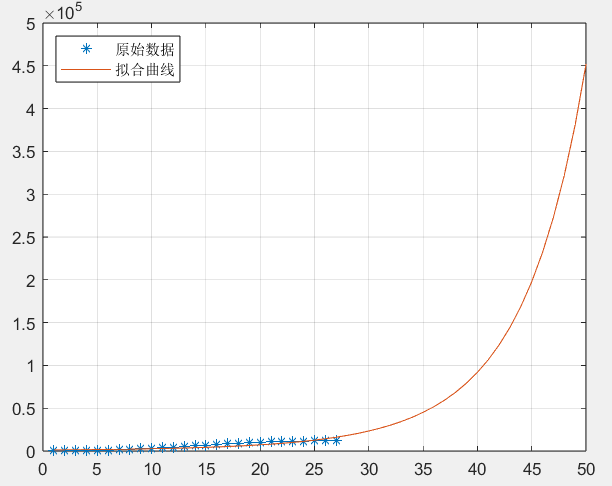
变化函数为x(t)=5.3087^(e^(0.0151t+1.6735)),最终规模可覆盖所有人,预计历时324天。
》》》》》》如有差错,还请各位小主原谅《《《《《《
68747470733a2f2f62:6c6f672e6373646e2e6e65742f71715f37353138353834362f:61727469636c652f64657461696c732f313335373537323037