控制工程中的数学建模（4）——控制系统时域数学模型建立的一般步骤（之一）

控制系统的数学模型是描述系统内部物理量之间关系的数学表达式。建立控制系统数学模型的方法有分析法和实验法。分析法是对系统各部分的运动机理进行分析，根据它们所依据的物理规律或化学规律分别列写相应的运动方程。实验法是人为地给系统施加某种测试信号，记录其输出响应，并用适当的数学模型去逼近，这种方法称为系统辨识。

时域中常用的数学模型有微分方程、差分方程和状态方程。我们采用分析法介绍微分方程数学模型。

微分方程的表现形式：

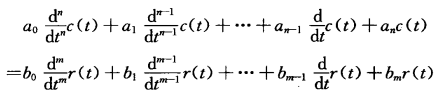
若系数 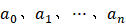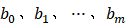； 是常数，称为定常系统。

第一步：线性元件的微分方程

一个复杂的控制系统必定包含多个线性的基础元件，这些元件有电气元件、电磁元件、力学元件、液压元件等。

我们来研究一个弹簧——质量——阻尼器机械位移子系统元件。这个子系统在控制阀体的阀芯开合位移上经常用到：

（1）明确子系统的输入输出量

列写质量块m在外力 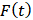作用下，位移 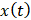的运动方程。

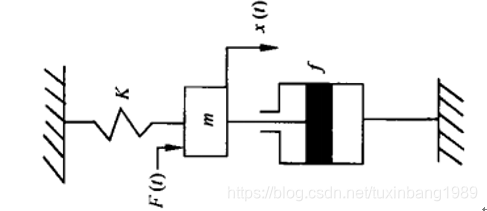
弹簧-质量-阻尼器机械位移子系统

（2）根据物理原理，列写等式，并引出中间量

质量块m相对于初始状态的位移为 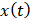，其速度

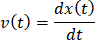
加速度

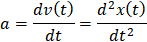
根据牛二定律

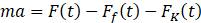
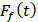——阻尼力，其方向与运动方向相反，大小与运动速度成比例，如摩擦力、液动力：

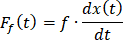
f ——阻尼系数。

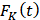——弹簧弹力，方向与运动方向相反，大小与位移成比例：

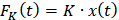
K——弹性系数。

（3）消去中间量，得到标准的微分方程

代入牛二定律等式，整理后得

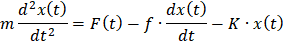
子系统的微分方程即为

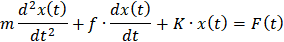
子系统的输入量为外力 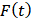，输出量为质量块m的位移 。

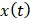根据上面实例分析，我们总结列写元件微分方程的步骤：

①由工作原理和控制目的，确定输入量和输出量；

②分析元件工作的物理或化学规律，列写相应的微分方程；

③消去中间变量，仅得到输出量与输入量之间关系的微分方程，此即为元件的时域模型。