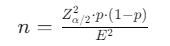2024-年高教社杯全国大学生数学建模竞赛B题4小问解题思路第二版

目录
2024 年高教社杯全国大学生数学建模竞赛B题4小问解题思路(第二版)
原文链接:
问题 1:抽样检测方案设计
详细解题思路:
- 确定抽样检测目标 :企业需要确定一个可接受的次品率上限(标称值),以及在该次品率下,企业愿意接受或拒绝零配件的信度水平(置信度)。
- 选择抽样方案 :根据信度要求,选择合适的抽样方案。常见的抽样方案包括简单随机抽样和分层抽样。
- 计算抽样大小 :根据次品率的标称值、信度水平和风险水平,计算所需的最小抽样大小。
- 确定接受/拒绝标准 :根据抽样结果,确定一个阈值,如果抽样中发现的次品数量超过这个阈值,则拒绝整批零配件。
- 模拟和验证 :通过模拟抽样过程,验证所设计的抽样方案是否满足企业的要求。
数学模型和公式:
二项分布 :假设零配件的次品率 p 是已知的,那么抽样中发现次品的数量 XX 服从二项分布 X∼B(n,p),其中 n 是抽样大小。
抽样大小计算 :可以使用以下公式来估计抽样大小 n:

其中,Zα/2 是正态分布的分位数,E 是可接受的误差范围。
接受/拒绝标准 :设定一个临界值 cc,如果 X>cX>c,则拒绝零配件。临界值可以通过以下公式计算: c=max{k:P(X≤k)≥1−β} 其中,ββ 是犯第一类错误的概率(即错误地接受不合格的零配件)。
示例代码:
from scipy.stats import binom
# 参数设置
p_nominal = 0.10 # 标称次品率
confidence_level = 0.95 # 信度水平
risk_level = 0.10 # 风险水平
error_margin = 0.05 # 可接受的误差范围
# 计算Z值
Z = abs((1 - confidence_level) ** 0.5)
# 计算抽样大小
n = (Z**2 * p_nominal * (1 - p_nominal)) / (error_margin**2)
# 计算接受/拒绝标准
c = binom.ppf(1 - risk_level, n, p_nominal)
# 输出结果
print(f"抽样大小: {int(n)}")
print(f"接受/拒绝标准: {int(c)}")
# 模拟抽样过程
sample_size = int(n)
defective_rate = p_nominal
samples = binom.rvs(n=sample_size, p=defective_rate, size=1000)
accept = samples <= c
# 计算接受率
accept_rate = accept.mean()
print(f"在标称次品率下,接受率: {accept_rate:.2f}")问题 2:生产过程决策
详细解题思路:
定义决策变量 :
- D1 和 D2:是否对零配件1和零配件2进行检测。
- T:是否对装配好的成品进行检测。
- R:是否对检测出的不合格成品进行拆解。
成本和收益分析 :
- 计算每个决策变量的成本和收益,包括检测成本、装配成本、市场售价、调换损失和拆解费用。
建立目标函数 :
- 最大化利润或最小化成本。
约束条件 :
- 零配件和成品的次品率。
- 检测和拆解的可行性。
模型求解 :
- 使用线性规划、动态规划或决策树来求解模型。
数学模型和公式:
目标函数 : Maximize Profit=Revenue−Cost 其中,Revenue 是销售合格成品的收入,Cost 包括购买成本、检测成本、装配成本、市场售价、调换损失和拆解费用。
约束条件 :
- 零配件合格率约束: P1≥(1−Defective Rate of Component 1)P2≥(1−Defective Rate of Component 2)
- 成品合格率约束: P≥(1−Defective Rate of Final Product)
决策变量 :
- D1,D2∈{0,1}:是否检测零配件。
- T∈{0,1}:是否检测成品。
- R∈{0,1}:是否拆解不合格成品。
示例代码:
import pulp
# 定义问题
prob = pulp.LpProblem("Production_Decision", pulp.LpMaximize)
# 定义决策变量
D1 = pulp.LpVariable("D1", cat='Binary')
D2 = pulp.LpVariable("D2", cat='Binary')
T = pulp.LpVariable("T", cat='Binary')
R = pulp.LpVariable("R", cat='Binary')
# 参数设置
cost_component1 = 4
cost_component2 = 18
cost_assembly = 6
cost_test_component1 = 2
cost_test_component2 = 3
cost_test_final = 3
cost_disassembly = 5
market_price = 56
replacement_loss = 6
# 成本函数
cost = cost_component1 * (1 - D1) + cost_component2 * (1 - D2) + cost_assembly + \
(D1 * cost_test_component1) + (D2 * cost_test_component2) + (T * cost_test_final) + \
(R * cost_disassembly)
# 收益函数
revenue = market_price * (1 - 0.1) * (1 - 0.1) * (1 - T)
# 目标函数
prob += revenue - cost
# 约束条件
prob += D1 + D2 + T + R <= 4, "Total_Tests"
# 求解问题
prob.solve()
# 输出结果
print("Status:", pulp.LpStatus[prob.status])
print("Optimal Decision Variables:")
print("D1 (Test Component 1) =", D1.varValue)
print("D2 (Test Component 2) =", D2.varValue)
print("T (Test Final Product) =", T.varValue)
print("R (Disassemble Rejected Products) =", R.varValue)
print("Maximum Profit =", pulp.value(prob.objective))问题 3:多道工序决策
详细解题思路:
定义决策变量 :
- 对于每个零配件 i ,定义 D i 为是否检测该零配件。
- 对于每个半成品 j ,定义 Aj 为是否检测该半成品。
- 对于成品,定义 T 为是否检测成品。
成本和收益分析 :
- 计算每个决策变量的成本和收益,包括购买成本、检测成本、装配成本、市场售价、调换损失和拆解费用。
建立目标函数 :
- 最大化利润或最小化成本。
约束条件 :
- 零配件和半成品的次品率。
- 检测和拆解的可行性。
模型求解 :
- 使用多阶段决策过程或网络流模型来求解模型。
数学模型和公式:
目标函数 : Maximize Profit=Revenue−Cost 其中,Revenue 是销售合格成品的收入,Cost 包括购买成本、检测成本、装配成本、市场售价、调换损失和拆解费用。
约束条件 :
- 零配件合格率约束: P i ≥(1−Defective Rate of Component i )
- 半成品合格率约束: Q j ≥(1−Defective Rate of Semi-finished Product j )
- 成品合格率约束: P≥(1−Defective Rate of Final Product)
决策变量 :
- D i ,A j ,T∈{0,1}:是否检测相应的零配件、半成品或成品。
示例代码:
import pulp
# 定义问题
prob = pulp.LpProblem("Multistage_Production_Decision", pulp.LpMaximize)
# 定义决策变量
components = ['1', '2', '3', '4', '5', '6', '7', '8']
D = pulp.LpVariable.dicts("D", components, cat='Binary')
A = pulp.LpVariable.dicts("A", components[0:4], cat='Binary') # 假设只有前4个组件形成半成品
T = pulp.LpVariable("T", cat='Binary')
# 参数设置
cost_component = {i: 2 for i in components} # 假设所有组件购买成本为2
cost_assembly = 8
cost_test = {i: 1 for i in components} # 假设所有组件检测成本为1
cost_test_final = 6
cost_disassembly = 4
market_price = 200
replacement_loss = 40
# 成本函数
cost = sum(cost_component[i] * (1 - D[i]) for i in components) + \
sum(cost_test[i] * D[i] for i in components) + \
sum(cost_test[i] * A[i] for i in components[0:4]) + \
cost_test_final * T + cost_disassembly * T
# 收益函数
revenue = market_price * (1 - 0.1) # 假设成品次品率为10%
# 目标函数
prob += revenue - cost
# 约束条件
for i in components:
prob += D[i] + A[i] + T <= 4, f"Total_Tests_{i}"
# 求解问题
prob.solve()
# 输出结果
print("Status:", pulp.LpStatus[prob.status])
print("Optimal Decision Variables:")
for i in components:
print(f"D_{i} (Test Component {i}) =", D[i].varValue)
for i in components[0:4]:
print(f"A_{i} (Test Semi-finished Product {i}) =", A[i].varValue)
print("T (Test Final Product) =", T.varValue)
print("Maximum Profit =", pulp.value(prob.objective))问题 4:考虑抽样误差的决策
详细解题思路:
考虑抽样误差 :
- 抽样误差会影响对零配件、半成品和成品次品率的估计。
- 需要考虑抽样误差对决策的影响,包括对检测和拆解决策的影响。
建立概率模型 :
- 使用概率模型来描述次品率的不确定性,例如使用贝叶斯方法或置信区间。
优化模型 :
- 建立一个优化模型,考虑不确定性下的决策,以最大化期望利润或最小化期望成本。
鲁棒性分析 :
- 评估在不确定性下,决策方案的鲁棒性,确保在最坏情况下仍能保持合理的性能。
模型求解 :
- 使用蒙特卡洛模拟或其他随机优化方法来求解模型。
数学模型和公式:
概率模型 :
- 假设次品率 p 是一个随机变量,可以使用贝叶斯方法来更新其后验分布。
优化模型 :
- 建立一个期望值模型,最大化期望利润: Maximize E[Profit]=E[Revenue]−E[Cost]
- 其中,E[Revenue] 和 E[Cost] 分别是收入和成本的期望值。
鲁棒性分析 :
- 使用最坏情况分析或敏感性分析来评估决策方案在不确定性下的表现。
示例代码:
import numpy as np
import pulp
# 定义问题
prob = pulp.LpProblem("Robust_Production_Decision", pulp.LpMaximize)
# 定义决策变量
D = pulp.LpVariable.dicts("D", [1, 2], cat='Binary')
T = pulp.LpVariable("T", cat='Binary')
# 参数设置
cost_component = [4, 18]
cost_test = [2, 3]
cost_assembly = 6
cost_test_final = 3
cost_disassembly = 5
market_price = 56
replacement_loss = 6
# 次品率和抽样误差
defective_rates = [0.1, 0.2] # 真实次品率
sample_sizes = [50, 50] # 抽样大小
sampling_error = 0.05 # 抽样误差
# 模拟抽样过程
np.random.seed(0)
sampled_defective_rates = np.random.normal(defective_rates, sampling_error, (2, 2))
# 成本函数
cost = (cost_component[0] * (1 - D[1]) + cost_test[0] * D[1] +
cost_component[1] * (1 - D[2]) + cost_test[1] * D[2] +
cost_assembly + cost_test_final * T)
# 收益函数
revenue = market_price * (1 - np.mean(sampled_defective_rates[:, 0])) * (1 - np.mean(sampled_defective_rates[:, 1]))
# 目标函数
prob += revenue - cost
# 约束条件
prob += D[1] + D[2] + T <= 3, "Total_Tests"
# 求解问题
prob.solve()
# 输出结果
print("Status:", pulp.LpStatus[prob.status])
print("Optimal Decision Variables:")
print("D1 (Test Component 1) =", D[1].varValue)
print("D2 (Test Component 2) =", D[2].varValue)
print("T (Test Final Product) =", T.varValue)
print("Maximum Profit =", pulp.value(prob.objective))