《数据结构与算法》编程题：斐波那契数列

题目描述如下：

分治策略是算法设计的重要策略之一，该策略的基本思想是把问题进行分解成一些子问题，通过子问题的求解完成对原问题的求解。其关键是分解和合并，好的分解或合并方法才会产生高效的分治算法。

分治策略设计出的算法最常见的就是递归算法。但是如果在分解时，分解出的子问题有很多是重复的，那么这样的分治（递归）算法求解问题的效率就非常低。例如斐波那契数问题，如果采用递归求解，算法效率非常低：O( 2n )。而如果采用递推求解(动态规划自底向上求解)，算法效率非常高：O(n)。

现在请你编写程序，统计计算一个斐波那契数时分解出的各子问题的个数。

斐波那契数的定义如下：

Fib(0)=0

Fib(1)=1

Fib(n)=Fib(n-1)+Fib(n-2)

输入： 一个整数n，即计算Fib(n)

输出：n+1行，即各个子问题的值及该子问题的个数。

例如

输入：

5

输出：

Fib(0)=0,spn=3

Fib(1)=1,spn=5

Fib(2)=1,spn=3

Fib(3)=2,spn=2

Fib(4)=3,spn=1

Fib(5)=5,spn=1

注：spn是该子问题的个数。

这道题目有点坑，题目说用递归效率很低，用递推效率就非常高，它的意思就是想鼓动你用递推算法解决这道题目，用递推算法算斐波那契数的值很好算，但是算子问题的个数很不好算，所以最后还是要用递归算法求解子问题的个数。这里大家可能对spn的取值有所疑惑，看下面的这张图再加上我的解释大家就明白了：

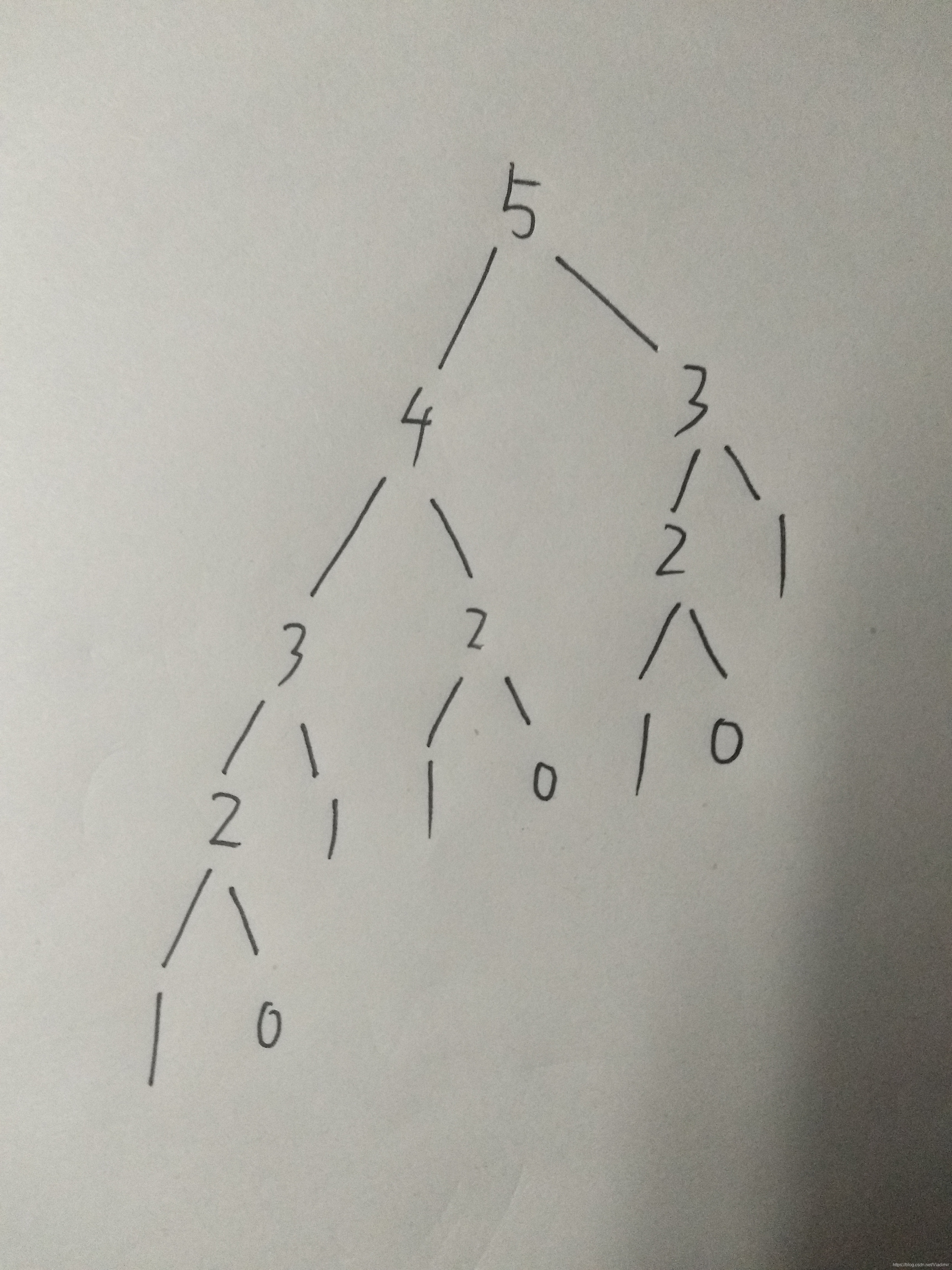
（字写得不太好，大家见谅哈）

从上面这张图可以看出， “1”有五个，“0”有四个，“2”有三个，“3”有两个，“4”和“5”各有一个，数量对应spn的数量，上述这张图就是斐波那契数列的子问题分解图。大家如果还有什么不明白的话可以在下方留言。

下面给出求解本题的C++完整代码：

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#define MAX 10005
using namespace std;

int result[MAX] = {0};//存储各个斐波那契数的结果
int spn[MAX] = {0};//存储相应的子问题个数
//递归函数求斐波那契数列的子问题个数
int fib(int n){
    spn[n]++;
    if(n==0){return 0;}
    else if(n==1){return 1;}
    return fib(n-1)+fib(n-2);
}
int main()
{
    int n;
    scanf("%d",&n);
    result[0] = 0;
    result[1] = 1;

    int i;
    //递推算法求斐波那契数列的值
    for(i=0;i<=n;i++){
        if(i==0){continue;}
        else if(i==1){continue;}
        else{
            result[i] = result[i-1] + result[i-2];
        }
    }
    fib(n);
    //按照要求打印结果
    for(i=0;i<=n;i++){
        printf("Fib(%d)=%d,spn=%d\n",i,result[i],spn[i]);
    }
    return 0;
}