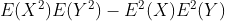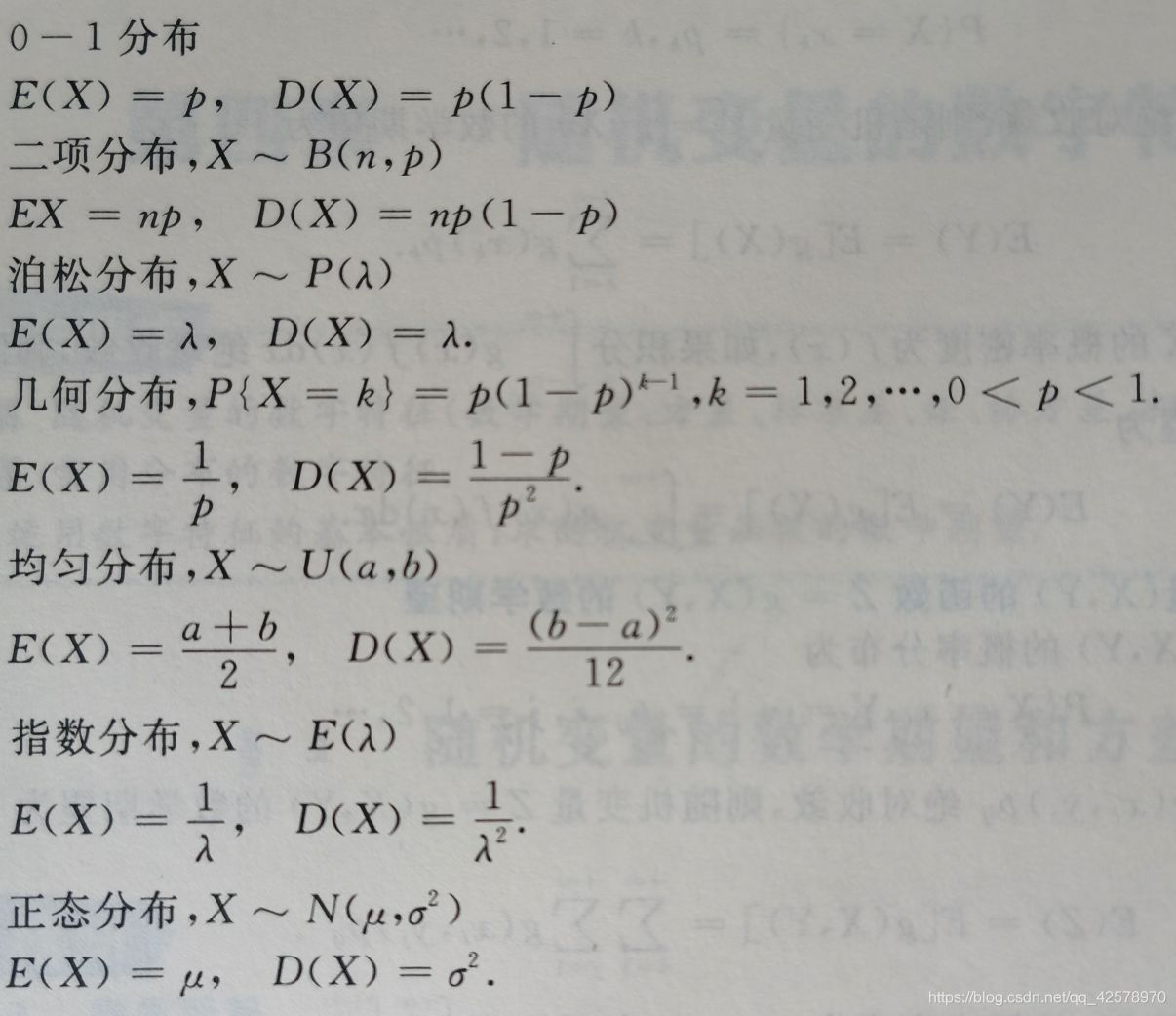数学期望与方差

数学期望 ：E(X)=

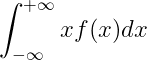
若Z=g(x,y)，x，y的概率密度函数为f(x,y)，则

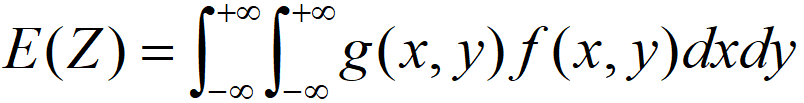
公式和技巧：

1.E(CX)=CE(X)

2.E(X Y)=E(X) E(Y)

3.E(XY)=E(X)E(Y)+ 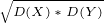*cov(X,Y)

4.如果一次实验的结果由多个独立实验的结果求和得到（例如随机投掷三次同一个骰子，求三次扔出来的数之和的数学期望），那么最终结果的数学期望为每一个独立实验的数学期望之和（因为每次投骰子，数学期望为3.5，那么三次之和为3*3.5=10.5）

5.E(X^2)的计算公式为

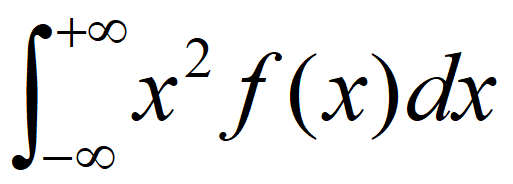
其他次数同理，不要直接把E(X)的公式套过来用了，f(x)也要根据计算有相应的改变

方差 ：D(X)=E(X^2)-E(X)^2

公式和技巧：

1.D(C)=0

2.D(aX+b)=a^2D(X)

3.D(X Y)=D(X)+D(Y) 2cov(X,Y)

4.D(XY)=E{[XY-E(XY)]^2}=