2025-01-09-神经网络架构搜索可微分搜索DARTS

神经网络架构搜索——可微分搜索(DARTS)
神经网络架构搜索——可微分搜索(DARTS)
背景
神经网络架构搜索之前主流的方法主要包括:强化学习,进化学习。他们的搜索空间都是不可微的,Differentiable Architecture Search 这篇文章提出了一种可微的方法,可以 用梯度下降来解决架构搜索的问题 ,所以在搜索效率上比之前不可微的方法快几个数量级。可以这样通俗的理解:之前不可微的方法,相当于是你定义了一个搜索空间(比如3x3和5x5的卷积核),然后神经网络的每一层你可以从搜索空间中选一种构成一个神经网络,跑一下这个神经网络的训练结果,然后不断测试其他的神经网络组合。这种方法,本质上是从很多的组合当中尽快的搜索到效果很好的一种,但是这个过程是黑盒,需要有大量的验证过程,所以会很耗时。而这篇文章把 架构搜索融合到模型当中一起训练 。
算法核心思想

由上图可分析:
- (a) 定义了一个cell单元,可看成 有向无环图 ,里面4个node,node之间的edge代表可能的操作(如:3x3 sep 卷积),初始化时unknown。
- (b) 把搜索空间 连续松弛化 ,每个edge看成是所有子操作的混合(softmax权值叠加)。
- © 联合优化 ,更新子操作混合概率上的 edge超参 (即架构搜索任务)和 架构无关的 网络参数 。
- (d) 优化完毕后,inference 直接 取概率最大的子操作 即可。
搜索空间
DARTS要做的事情,是 训练出来两个Cell(Norm-Cell和Reduce-Cell) ,然后把 Cell相连构成一个大网络 ,而超参数layers可以控制有多少个cell相连,例如layers = 20表示有20个cell前后相连。
- Norm-Cell: [输入与输出的FeatureMap尺寸保持一致]
- Reduce-Cell: [输出的FeatureMap尺寸减小一半]
Cell的组成
Cell由输入节点,中间节点,输出节点,边四部分构成,我们规定每一个cell有 两个输入节点 和 一个输出节点 ,Norm-Cell和Reduce-Cell的结构相同,不过操作不同。
- 输入节点:对于卷积网络来说,两个输入节点分别是前两层(layers)cell的输出,对于循环网络(Recurrent)来说,输入时当前层的输入和前一层的状态。
- 中间节点:每一个中间节点都由它的前继通过边再求和得来。
- 输出节点:由每一个中间节点concat起来。
- 边:边代表的是operation(比如3*3的卷积),在收敛得到结构的过程中,两两节点中间所有的边(DARTS 预定义了8中不同的操作 )都会存在并参与训练,最后加权平均,这个权就是我们要训练的东西,我们希望得到的结果是效果最好的边它的权重最大。
DARTS实际预定义的Cell结构与论文中示意图的表示略有不同,完整的Cell结构包含两个输入节点,四个中间节点和一个输出节点,如下图所示:

全连接的情况下,N0中间节点有两个前继节点;N1,N2,N3分别有3,4,5个前继节点。每个节点之间有对应8个不同的预定义操作,共同构成一组边。
首先我们定义如下公式用softmax归一化alpha处理一组边:
o ˉ ( i , j ) ( x )
∑ o ∈ O exp ( α o ( i , j ) ) ∑ o ′ ∈ O exp ( α o ′ ( i , j ) ) o ( x ) \bar{o}^{(i, j)}(x)=\sum_{o \in \mathcal{O}} \frac{\exp \left(\alpha_{o}^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)} o(x)
o
ˉ
(
i
,
j
)
(
x
)
=
o
∈
O
∑
∑
o
′
∈
O
exp
(
α
o
′
(
i
,
j
)
)
exp
(
α
o
(
i
,
j
)
)
o
(
x
)
通过公式可知每个操作对应一个权值(即alpha),这就是我们要训练的参数,我们把这些alpha称作一个 权值矩阵 ,alpha值越大代表的操作在这组边中越重要。
然后每组中间节点公式表示如下,即所有前继节点累加作为当前节点的输出:
x ( i )
∑ j < i o ( i , j ) ( x ( j ) ) x^{(i)}=\sum_{j<i} o^{(i, j)}\left(x^{(j)}\right)
x
(
i
)
=
j
<
i
∑
o
(
i
,
j
)
(
x
(
j
)
)
我们收敛到最后希望得到一个权值矩阵,这个矩阵当中权值越大的边,留下来之后效果越好。
优化策略
通过前面定义的搜索空间,我们的目的是通过梯度下降优化 alpha矩阵 。我们把神经网络原有的权重称为 W矩阵 。为了实现端到端的优化,我们希望同时优化两个矩阵使得结果变好。 上述两层优化是有严格层次的 ,为了使两者都能同时达到优化的策略,一个朴素的想法是:在训练集上固定alpha矩阵的值,然后梯度下降W矩阵的值,在验证集上固定W矩阵的值,然后梯度下降alpha的值,循环往复直到这两个值都比较理想。这个过程有点像k-means的过程,先定了中心,再求均值,再换中心,再求均值。需要注意的是 验证集和训练集的划分比例是1:1的 ,因为对于alpha矩阵来说,验证集就是它的训练集。
min α L v a l ( w ∗ ( α ) , α ) s.t. w ∗ ( α )
argmin w L t r a i n ( w , α ) \begin{array}{cl} \min {\alpha} & \mathcal{L}{v a l}\left(w^{}(\alpha), \alpha\right) \ \text { s.t. } & w^{}(\alpha)=\operatorname{argmin}{w} \mathcal{L}{t r a i n}(w, \alpha) \end{array}
min
α
s.t.
L
v
a
l
(
w
∗
(
α
)
,
α
)
w
∗
(
α
)
=
a
r
g
m
i
n
w
L
t
r
a
i
n
(
w
,
α
)
但是这个方法虽然可以工作,但是效果不是很好,由于这种双优化的问题很难求得精确解(因为需要反复迭代求解两个参数),所以采用一种 近似的迭代优化步骤来交替更新两个参数 ,算法如下:

具体的公式推导流程可参考( )
∇ α L v a l ( ω ∗ ( α ) , α ) ≈ ∇ α L v a l ( ω − ξ ∇ ω L t r a i n ( ω , α ) , α ) \begin{aligned} \nabla_{\alpha} \mathcal{L}{v a l}\left(\omega^{*}(\alpha), \alpha\right) \ \approx \nabla{\alpha} \mathcal{L}{v a l}(&\left.\omega-\xi \nabla{\omega} \mathcal{L}_{t r a i n}(\omega, \alpha), \alpha\right) \end{aligned}
∇
α
L
v
a
l
(
ω
∗
(
α
)
,
α
)
≈
∇
α
L
v
a
l
(
ω
−
ξ
∇
ω
L
t
r
a
i
n
(
ω
,
α
)
,
α
)
∇ α L v a l ( ω − ξ ∇ ω L t r a i n ( ω , α ) , α )
∇ α L v a l ( ω ′ , α ) − ξ ∇ α , ω 2 L t r a i n ( ω , α ) ⋅ ∇ ω ′ L v a l ( ω ′ , α ) \begin{aligned} & \nabla_{\alpha} \mathcal{L}{v a l}\left(\omega-\xi \nabla{\omega} \mathcal{L}{t r a i n}(\omega, \alpha), \alpha\right) \ =& \nabla{\alpha} \mathcal{L}{v a l}\left(\omega^{\prime}, \alpha\right)-\xi \nabla{\alpha, \omega}^{2} \mathcal{L}{t r a i n}(\omega, \alpha) \cdot \nabla{\omega^{\prime}} \mathcal{L}_{v a l}\left(\omega^{\prime}, \alpha\right) \end{aligned}
=
∇
α
L
v
a
l
(
ω
−
ξ
∇
ω
L
t
r
a
i
n
(
ω
,
α
)
,
α
)
∇
α
L
v
a
l
(
ω
′
,
α
)
−
ξ
∇
α
,
ω
2
L
t
r
a
i
n
(
ω
,
α
)
⋅
∇
ω
′
L
v
a
l
(
ω
′
,
α
)
∇ α , w 2 L t r a i n ( w , α ) ∇ w ′ L v a l ( w ′ , α ) ≈ ∇ α L t r a i n ( w + , α ) − ∇ α L t r a i n ( w − , α ) 2 ϵ \nabla_{\alpha, w}^{2} \mathcal{L}{t r a i n}(w, \alpha) \nabla{w^{\prime}} \mathcal{L}{v a l}\left(w^{\prime}, \alpha\right) \approx \frac{\nabla{\alpha} \mathcal{L}{t r a i n}\left(w^{+}, \alpha\right)-\nabla{\alpha} \mathcal{L}_{t r a i n}\left(w^{-}, \alpha\right)}{2 \epsilon}
∇
α
,
w
2
L
t
r
a
i
n
(
w
,
α
)
∇
w
′
L
v
a
l
(
w
′
,
α
)
≈
2
ϵ
∇
α
L
t
r
a
i
n
(
w
,
α
)
−
∇
α
L
t
r
a
i
n
(
w
−
,
α
)
生成最终Cell结构
根据前面所述,我们要训练出来一个alpha矩阵,使得权重大的边保留下来,所以在这个结构收敛了之后还需要做一个生成最终Cell的过程。那这个时候你可能会问,为什么不把之前的结构直接用上呢?因为边太多,结构太复杂,参数太多不好训练,所以作者希望能生成一个更简单的网络结构,接下来我们说生成的方法。
对于 每一个中间节点来说,我们最多保留两个最强壮的前继 ;对于 两两节点之间的边,我们只保留权重最大的一条边 ,我们定义一下什么是最强壮的前继。假设一个节点有三个前继,那我们选哪两个呢?把前继和当前节点之间权重最高的那条边代表那个前继的强壮程度,我们选最强壮的两个前继。节点之间只保留权重最大的那条边。

normal cell search
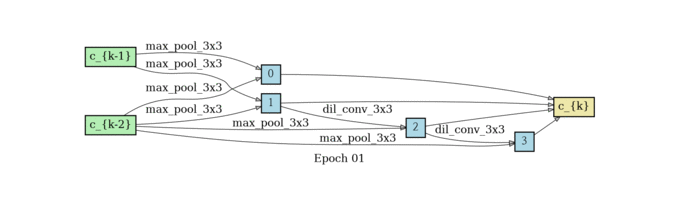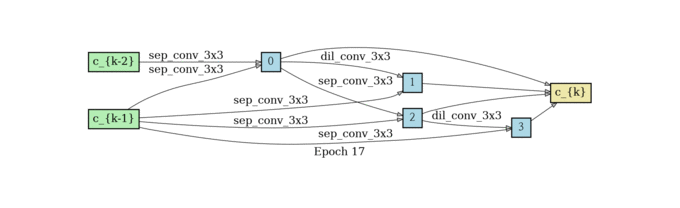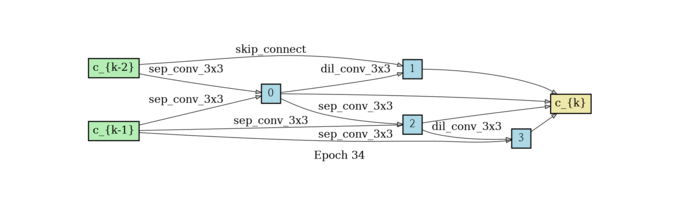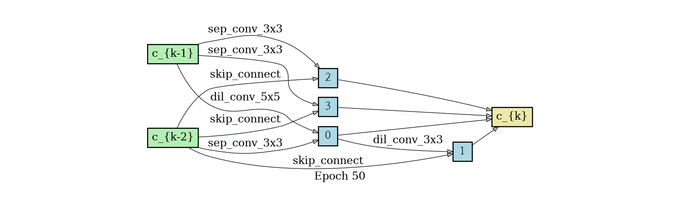
reduce cell search
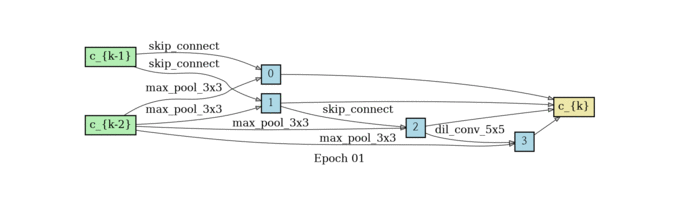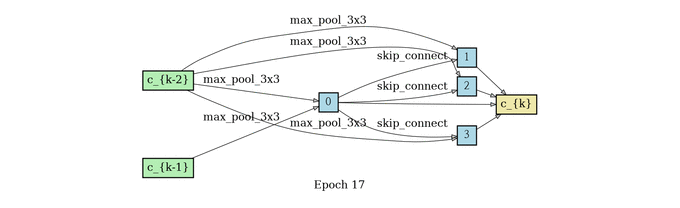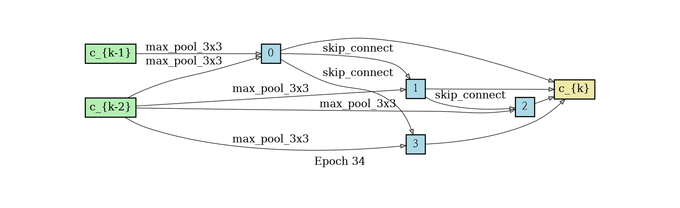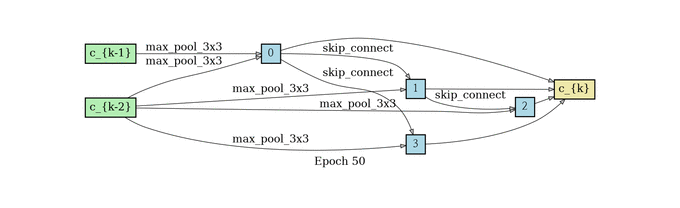
网络结构堆叠
下图,展示了Normal-Cell与Reduce-Cell的连接方式,代码描述是在1/3处和2/3处添加两个Reduce-Cell。比如,在CIFAR-10数据集上的网络结构需要20个Cell串联。
NetWork=6*Normal-Cell+Reduce-Cell+6*Normal-Cell+Reduce-Cell+6*Normal-Cell

由于,Cell结构是两个输入的,因此详细的Cell连接方式如下所示:

结果
CIFAR-10

ImageNet

参考
Liu, H., Simonyan, K., & Yang, Y. (2019). DARTS: Differentiable Architecture Search. ArXiv, abs/1806.09055.

68747470733a2f2f:626c6f672e6373646e2e6e65742f753031323334373032372f:61727469636c652f64657461696c732f313036313735303230