技术博客
首页 所有文章 标签 分类 关于
技术博客

目录

二叉搜索树的创建,删除,查找

 收录于 数据结构 C
   约 3140 字   预计阅读 7 分钟 
https://bing.ee123.net/img/rand?artid=82312723

二叉搜索树的创建，删除，查找

二叉搜索树的概念

二叉搜索树又称二叉排序树，它或者是一颗空树，或者是具有以下性质的二叉树

  • 若它的左子树不为空，则左子树上的所有结点的值都小于根结点的值。
  • 若它的右子树不为空，则右子树上的所有结点的值都大于根节点的值。
  • 它的左右子树也分别为二叉搜索树。 https://i-blog.csdnimg.cn/blog_migrate/898e5657eac9c02f3f2cdf2ff6f8bef0.jpeg
二叉搜索树的操作

查找关键字data： ①.若根节点为空，即二叉搜索树为空。返回0。 ②.若data>根节点的data，在其右子树查找；若data<根节点的data，在其左子树查找；若data==根节点的data，返回1；找不到返回0。

int FindBSTree(BSTree *BStree, BSDataType data)
{
BSTree *cur = BStree;
//根节点为空，即二叉树为空，返回0
if (BStree == NULL)
{
return 0;
}
while (cur != NULL)
{
if (cur->_data == data)
{
return 1;
}
else if (cur->_data > data)
{
cur = cur->_pleft;
}
else
cur = cur->_pright;
}
//cur==NULL即没有找到元素和data相等，返回0
return 0;
}

递归查找

//递归查找
int FindBSTree(BSTree *BStree, BSDataType data)
{
BSTree *cur = BStree;
if (BStree == NULL)
{
return 0;
}
if (cur->_data == data)
{
return 1;
}
else if (cur->_data > data)
{
return FindBSTree(BStree->_pleft,data);
}
else
{
return FindBSTree(BStree->_pright, data);
}
}

插入元素data： 在二叉树中插入元素时，必须检测该元素在树中是否已经存在，若存在则不进行插入。 ①.树为空，即二叉树为空时直接插入。 ②.树不为空，若data>根节点的data，在右子树插入；若data<根节点的data，在其左子树插入；若data==根节点的data，返回0，不插入； 在找要插入的位置的时候始终记录双亲结点。 ③.找到要插入的位置之后，判断双亲结点的data和要插入的data的大小，若data>双亲结点的data，则插入右子树，否则插入左子树。

//插入
int InsertBSTree(BSTree **BStree, BSDataType data)
{
BSTree *cur = NULL;
BSTree *parent = NULL;
assert(BStree);
cur = *BStree;
//1.若二叉树为空
if (NULL == *BStree)
{
*BStree = BuyNode(data);
}
//2.若二叉树不为空
else
{
//①.寻找插入的位置
while (cur != NULL)
{
parent = cur;
if (data < cur->_data)
{
cur = cur->_pleft;
}
else if (data > cur->_data)
{
cur = cur->_pright;
}
else
{
return 0;
}
}
//②.建立新结点
cur = BuyNode(data);
//③.data若比双亲大，则插右边，若比双亲小，则插左边
if (data < parent->_data)
{
parent->_pleft = cur;
}
else
{
parent->_pright = cur;
}
}
return 1;
}

递归插入：

int InsertBSTree(BSTree **BStree, BSDataType data)
{
BSTree *cur = NULL;
BSTree *parent = NULL;
assert(BStree);
cur = *BStree;
if (NULL == *BStree)
{
*BStree = BuyNode(data);
}
else
{
if (data > cur->_data)
{
return InsertBSTree(&(*BStree)->_pright, data);
}
else if (data < cur->_data)
{
return InsertBSTree(&(*BStree)->_pleft, data);
}
else
{
return 0;
}
}
return 1;
}

删除元素data： 在二叉树中删除元素时，必须检测该元素在树中是否已经存在，若不存在则直接返回0，不删除。若存在又分为以下四种情况：

  1. 要删除的结点无孩子结点（叶子结点）。
  2. 要删除的结点只有右孩子结点。
  3. 要删除的结点只有左孩子结点。
  4. 要删除的结点有左,右孩子结点。 情况1可以和情况2或者情况3合并，对于上述情况，相应的删除方法有： ① 直接删除该结点 ② 删除该结点且被删除结点的双亲结点指向被删除孩子的右孩子结点。 ③ 删除该结点且被删除结点的双亲结点指向被删除孩子的左孩子结点。 ④ 在它的右子树中寻找最小的结点，用它的值替换被删除结点的值。
int DeleteBSTree(BSTree **BStree, BSDataType data)
{
BSTree *cur = NULL;
BSTree *del = NULL; //要删除的结点
BSTree *parent = NULL; //要删除结点的双亲结点
assert(BStree);
cur = *BStree;
if (*BStree == NULL)
{
return 0;
}
//寻找要删除的点
while (cur != NULL)
{
if (cur->_data == data)
{
break;
}
else if (data < cur->_data)
{
parent = cur;
cur = cur->_pleft;
}
else
{
parent = cur;
cur = cur->_pright;
}
}
if (cur == NULL)
{
//证明要删除的元素不在二叉搜索树内
return 0;
}
//只有右孩子或者叶子
if (cur->_pleft == NULL)
{
//如果是根节点，让根节点指向它的右子树
if (cur == *BStree)
{
*BStree = (*BStree)->_pright;
}
else
{
//判断cur是双亲的左孩子还是右孩子
//双亲指向cur的右孩子，因为左孩子为空
if (parent->_pleft == cur)
{
parent->_pleft = cur->_pright;
}
else
{
parent->_pright = cur->_pright;
}
}
}
//只有左孩子
else if (cur->_pright == NULL)
{
//如果是根节点，让根节点指向它的左子树
if (cur == *BStree)
{
*BStree = (*BStree)->_pleft;
}
else
{
//判断cur是双亲的左孩子还是右孩子
//双亲指向cur的左孩子，因为右孩子为空
if (parent->_pleft == cur)
{
parent->_pleft = cur->_pleft;
}
else
{
parent->_pright = cur->_pleft;
}
}
}
//左右孩子均存在
else
{
del = cur->_pright;
parent = cur;
//找到右子树里面最小的一个，覆盖要删除的结点
while (del->_pleft)
{
parent = del;
del = del->_pleft;
}
//将找到的结点的值赋给要删除的结点
cur->_data = del->_data;
//删除replace
if (parent->_pleft == del)
{
parent->_pleft = NULL;
cur = del;
}
else
{
parent->_pright = NULL;
cur = del;
}
}
free(cur);
cur = NULL;
return 1;
}

递归删除

int DeleteBSTree(BSTree **BStree, BSDataType data)
{
BSTree *del = NULL;
BSTree *cur = NULL;
assert(BStree);
if ((*BStree) == NULL)
{
return 0;
}
if (data < (*BStree)->_data )
{
return DeleteBSTree(&(*BStree)->_pleft,data);
}
else if (data > (*BStree)->_data )
{
return DeleteBSTree(&(*BStree)->_pright, data);
}
else
{
cur = *BStree;
if ((*BStree)->_pleft == NULL)
{
*BStree = (*BStree)->_pright;
free(cur);
cur = NULL;
}
else if ((*BStree)->_pright == NULL)
{
*BStree = (*BStree)->_pleft;
free(cur);
cur = NULL;
}
else
{
del = (*BStree)->_pright;
while (del->_pleft)
{
del = del->_pleft;
}
(*BStree)->_data = del->_data;
return DeleteBSTree(&(*BStree)->_pright, del->_data);
}
}
return 1;
}
整体代码：

.h文件

#include
#include
#include
#include
//二叉树的结构
typedef int BSDataType;
typedef struct BSTree
{
struct BSTree *_pleft;
struct BSTree *_pright;
BSDataType _data;
}BSTree;
//初始化
void InitBSTree(BSTree **BSTree);
//插入
int InsertBSTree(BSTree **BSTree, BSDataType data);
//中序遍历
void InOrder(BSTree *BStree);
//删除
int DeleteBSTree(BSTree **BStree, BSDataType data);
//查找
int FindBSTree(BSTree *BStree, BSDataType data);
//销毁
void DestroyBSTree(BSTree **BStree);

.c文件

#include"BSTree.h"
//初始化
void InitBSTree(BSTree **BSTree)
{
assert(BSTree);
*BSTree = NULL;
}
BSTree* BuyNode(BSDataType d)
{
BSTree *newnode = (BSTree *)malloc(sizeof(BSTree));
if (NULL == newnode)
{
//若开辟空间失败，则打印出错误，不进行后面的代码
assert(0);
return NULL;
}
newnode->_data = d;
newnode->_pleft = NULL;
newnode->_pright = NULL;
return newnode;
}
插入
//int InsertBSTree(BSTree **BStree, BSDataType data)
//{
// BSTree *cur = NULL;
// BSTree *parent = NULL;
//
// assert(BStree);
// cur = *BStree;
// //1.若二叉树为空
// if (NULL == *BStree)
// {
// *BStree = BuyNode(data);
// }
// //2.若二叉树不为空
// else
// {
//
// //①.寻找插入的位置
// while (cur != NULL)
// {
// parent = cur;
// if (data < cur->_data)
// {
// cur = cur->_pleft;
// }
// else if (data > cur->_data)
// {
// cur = cur->_pright;
// }
// else
// {
// return 0;
// }
// }
// //②.建立新结点
// cur = BuyNode(data);
// //③.data若比双亲大，则插右边，若比双亲小，则插左边
// if (data < parent->_data)
// {
// parent->_pleft = cur;
// }
// else
// {
// parent->_pright = cur;
// }
// }
// return 1;
//}
//递归插入
int InsertBSTree(BSTree **BStree, BSDataType data)
{
BSTree *cur = NULL;
BSTree *parent = NULL;
assert(BStree);
cur = *BStree;
if (NULL == *BStree)
{
*BStree = BuyNode(data);
}
else
{
if (data > cur->_data)
{
InsertBSTree(&(*BStree)->_pright, data);
}
else if (data < cur->_data)
{
InsertBSTree(&(*BStree)->_pleft, data);
}
else
{
return 0;
}
}
return 1;
}
//中序遍历 左-->根-->右
void InOrder(BSTree *BStree)
{
if (BStree == NULL)
{
return;
}
InOrder(BStree->_pleft);
printf("%d ", BStree->_data);
InOrder(BStree->_pright);
}
删除
//int DeleteBSTree(BSTree **BStree, BSDataType data)
//{
// BSTree *cur = NULL;
// BSTree *del = NULL; //要删除的结点
// BSTree *parent = NULL; //要删除结点的双亲结点
// assert(BStree);
// cur = *BStree;
// if (*BStree == NULL)
// {
// return 0;
// }
// //寻找要删除的点
// while (cur != NULL)
// {
// if (cur->_data == data)
// {
// break;
// }
// else if (data < cur->_data)
// {
// parent = cur;
// cur = cur->_pleft;
// }
// else
// {
// parent = cur;
// cur = cur->_pright;
// }
// }
// if (cur == NULL)
// {
// //证明要删除的元素不在二叉搜索树内
// return 0;
// }
// //只有右孩子或者叶子
// if (cur->_pleft == NULL)
// {
// //如果是根节点，让根节点指向它的右子树
// if (cur == *BStree)
// {
// *BStree = (*BStree)->_pright;
// }
// else
// {
// //判断cur是双亲的左孩子还是右孩子
// if (parent->_pleft == cur)
// {
// parent->_pleft = cur->_pright;
// }
// else
// {
// parent->_pright = cur->_pright;
// }
// }
// }
// //只有左孩子
// else if (cur->_pright == NULL)
// {
// //如果是根节点，让根节点指向它的左子树
// if (cur == *BStree)
// {
// *BStree = (*BStree)->_pleft;
// }
// else
// {
// //判断cur是双亲的左孩子还是右孩子
// if (parent->_pleft == cur)
// {
// parent->_pleft = cur->_pleft;
// }
// else
// {
// parent->_pright = cur->_pleft;
// }
//
// }
// }
// //左右孩子均存在
// else
// {
// del = cur->_pright;
// parent = cur;
// //找到右子树里面最小的一个
// while (del->_pleft)
// {
// parent = del;
// del = del->_pleft;
// }
// //将找到的结点的值赋给要删除的结点
// cur->_data = del->_data;
// //删除replace
// if (parent->_pleft == del)
// {
// parent->_pleft = NULL;
// cur = del;
// }
// else
// {
// parent->_pright = NULL;
// cur = del;
// }
// }
// free(cur);
// cur = NULL;
// return 1;
//}
//递归删除
int DeleteBSTree(BSTree **BStree, BSDataType data)
{
BSTree *del = NULL;
BSTree *cur = NULL;
assert(BStree);
if ((*BStree) == NULL)
{
return 0;
}
if (data < (*BStree)->_data )
{
DeleteBSTree(&(*BStree)->_pleft,data);
}
else if (data > (*BStree)->_data )
{
DeleteBSTree(&(*BStree)->_pright, data);
}
else
{
cur = *BStree;
if ((*BStree)->_pleft == NULL)
{
*BStree = (*BStree)->_pright;
free(cur);
cur = NULL;
}
else if ((*BStree)->_pright == NULL)
{
*BStree = (*BStree)->_pleft;
free(cur);
cur = NULL;
}
else
{
del = (*BStree)->_pright;
while (del->_pleft)
{
del = del->_pleft;
}
(*BStree)->_data = del->_data;
DeleteBSTree(&(*BStree)->_pright, del->_data);
}
}
return 1;
}
//查找
int FindBSTree(BSTree *BStree, BSDataType data)
{
BSTree *cur = BStree;
//根节点为空，即二叉树为空，返回0
if (BStree == NULL)
{
return 0;
}
while (cur != NULL)
{
if (cur->_data == data)
{
return 1;
}
else if (cur->_data > data)
{
cur = cur->_pleft;
}
else
cur = cur->_pright;
}
//cur==NULL即没有找到元素和data相等，返回0
return 0;
}
递归查找
//int FindBSTree(BSTree *BStree, BSDataType data)
//{
// BSTree *cur = BStree;
// if (BStree == NULL)
// {
// return 0;
// }
// if (cur->_data == data)
// {
// return 1;
// }
// else if (cur->_data > data)
// {
// return FindBSTree(BStree->_pleft,data);
// }
// else
// {
// return FindBSTree(BStree->_pright, data);
// }
//}
//销毁二叉树
void DestroyBSTree(BSTree **BStree)
{
assert(BStree);
if (*BStree == NULL)
{
return;
}
DestroyBSTree(&(*BStree)->_pleft);
DestroyBSTree(&(*BStree)->_pright);
free(*BStree);
*BStree = NULL;
}

测试文件：

#include"BSTree.h"
void TestBSTree()
{
BSTree *BStree;
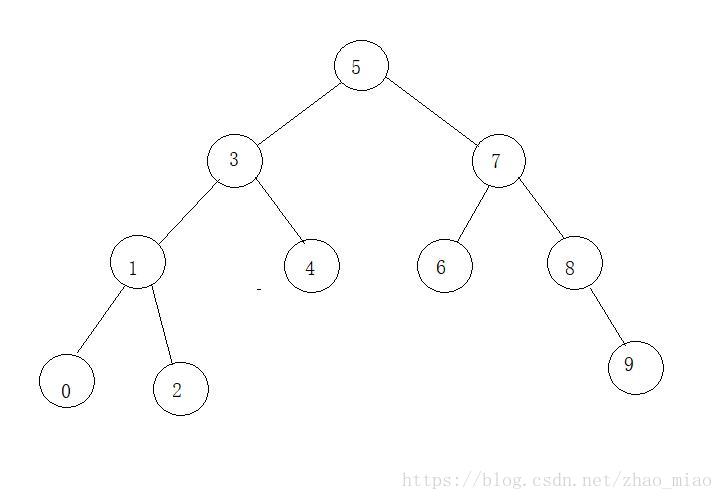
int a[] = { 5, 3, 4, 1, 7, 8, 2, 6, 0, 9 };
int i = 0;
//初始化二叉搜索树
InitBSTree(&BStree);
for (i = 0; i < sizeof(a) / sizeof(a[0]); i++)
{
//插入
InsertBSTree(&BStree, a[i]);
}
//插入
InsertBSTree(&BStree, 10);
//中序遍历
InOrder(BStree);
printf("\n");
//查找
if (FindBSTree(BStree, 1))
{
printf("找到了！\n");
}
else
{
printf("没找到!\n");
}
//查找
if (FindBSTree(BStree, -1))
{
printf("找到了！\n");
}
else
{
printf("没找到!\n");
}
//删除
DeleteBSTree(&BStree, 5);
//删除
DeleteBSTree(&BStree, 3);
//中序遍历
InOrder(BStree);
printf("\n");
//摧毁
DestroyBSTree(&BStree);
}
int main()
{
TestBSTree();
system("pause");
return 0;
}

https://i-blog.csdnimg.cn/blog_migrate/62488ed8002a508117612787e6ad4e3b.jpeg

更新于 2025-01-09
 二叉搜索树的添加, 二叉搜索树的查找, 二叉搜索树的删除, 二叉搜索树, 二叉排序树
返回 | 主页