C-搜索

C++ 搜索
程序设计实践课笔记。
搜索算法是利用计算机的高性能来有目的地穷举一个问题的部分或所有的可能情况,从而求出问题的解的一种方法,有一定的方向性和目标性。
状态(state)是对问题在某一时刻进展情况的数学描述,或者是数学抽象。
每一个状态都会是答案的一个“可能的”解。状态的转移就是问题从一个状态转移到另一个状态,这样就可以进行搜索的一步步延伸,最后要得到的解也是其中的一个状态。
广度优先搜索(BFS)
基本思想 :从初始状态S 开始,生成所有可能的状态。构成的下一层节点,检查是否出现目标状态G,若未出现,就对该层所有状态节点,分别顺序扩展。
生成再下一层的所有状态节点,对这一层的所有状态节点检查是否出现G,若未出现,继续按上面思想生成再下一层的所有状态节点,这样一层一层往下展开。直到出现目标状态为止。
——在路径的寻找问题上用得比较多
可以利用队列先进先出(FIFO)的性质:
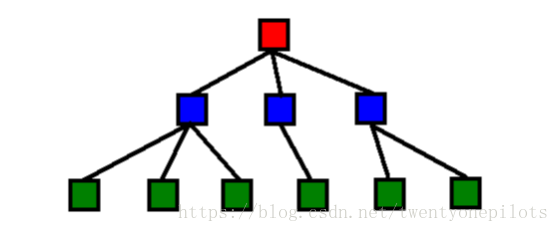
对应的队列:

具体过程:
1 每次取出队列首元素(初始状态),进行拓展
2 然后把拓展所得到的可行状态都放到队列里面
3 将初始状态删除
4 一直进行以上三步直到队列为空。
例一
农夫去追他跑丢的牛,题目给出了他和牛的位置,用数字N和K表示,假定牛不动,问农夫移动到牛的位置的最小步数,农夫每次的移动有三种选择:位置加1,位置减1,位置乘2。
#include <iostream>
#include<string.h>
#define mem(a) memset(a,0,sizeof(a))
using namespace std;
const int maxn=100000 +1;
int vis[maxn], q[maxn] , d[maxn];
int n , k ;
void bfs(int s,int e){
mem(vis);mem(q);mem(d);
vis[s]=1;
d[s]=0;
int q_start =0 , q_end = 0;
q[q_end++] = s ;
while(q_start<q_end){
s = q[q_start++];
if(s==e)return ;
if(s>0 && !vis[s-1]){
vis[s-1]=1;
q[q_end++]=s-1;
d[s-1]=d[s]+1;
}
if(s<maxn+1 && !vis[s+1]){
vis[s+1]=1;
q[q_end++]=s+1;
d[s+1]=d[s]+1;
}
if((s<maxn/2+1)&& !vis[2*s]){
vis[2*s]=1;
q[q_end++]=2*s;
d[2*s]=d[s]+1;
}
}
}
int main()
{
cin>>n>>k;
bfs(n,k);
cout<<d[k]<<endl;
return 0;
}例二
给出一三维空间的地牢,要求求出由字符’S’到字符’E’的最短路径。移动方向可以是上,下,左,右,前,后,六个方向。每移动一次就耗费一分钟,要求输出最快的走出时间。不同c层的地图,相同ab坐标处是连通的。
初稿,运行结果也不正确,主要看思想。
#include <iostream>
#include<string.h>
using namespace std;
char s[100][100][100];
int d[100][100][100];
int qa[100];
int qb[100];
int qc[100];
int main()
{
memset(d,0,sizeof(d));
int a,b,c;
int sa,sb,sc;
int ea,eb,ec;
cin>>a>>b>>c;
for(int i=0;i<a;i++){
for(int j=0;j<b;j++){
for(int k=0;k<c;k++){
cin>>s[i][j][k];
if(s[i][j][k]=='S'){
sa=i;sb=j;sc=k;
}
if(s[i][j][k]=='E'){
ea=i;eb=j;ec=k;
}
}
}
}
int qsa=0,qea=0,qsb=0,qeb=0,qsc=0,qec=0;
qa[qea++]=sa;
qb[qeb++]=sb;
qc[qec++]=sc;
int flag=0;
while(qsa<qea&&qsb<qeb&&qsc<qec){
sa=qa[qsa++];
sb=qb[qsb++];
sc=qc[qsc++];
if(sa==ea && sb==eb && sc==ec){
flag=1;
break;
}
if(sa<a-1&&s[sa+1][sb][sc]=='.'){
s[sa+1][sb][sc]='#';
qa[qea++]=sa+1;
d[sa+1][sb][sc]=d[sa][sb][sc]+1;
}
if(sa>0&&s[sa-1][sb][sc]=='.'){
s[sa-1][sb][sc]='#';
qa[qea--]=sa-1;
d[sa-1][sb][sc]=d[sa][sb][sc]+1;
}
if(sb<b-1&&s[sa][sb+1][sc]=='.'){
s[sa][sb+1][sc]='#';
qb[qeb++]=sb+1;
d[sa][sb+1][sc]=d[sa][sb][sc]+1;
}
if(sb>0&&s[sa][sb-1][sc]=='.'){
s[sa][sb-1][sc]='#';
qb[qeb--]=sb-1;
d[sa][sb-1][sc]=d[sa][sb][sc]+1;
}
if(sc<c-1&&s[sa][sb][sc+1]=='.'){
s[sa][sb][sc+1]='#';
qc[qec++]=sc+1;
d[sa][sb][sc+1]=d[sa][sb][sc]+1;
}
if(sc>0&&s[sa][sb][sc-1]=='.'){
s[sa][sb][sc-1]='#';
qc[qec--]=sc-1;
d[sa][sb][sc-1]=d[sa][sb][sc]+1;
}
}
if(!flag)cout<<"NO ANSWER"<<endl;
else cout<<d[ea][eb][ec]<<endl;
return 0;
}深度优先搜索(DFS)
基本思想 :从初始状态,生成搜索树下一层任一个结点,检查是否出现目标状态,若未出现,以此状态利用规则生成再下一层任一个结点,再检查,重复过程一直到叶节点(即不能再生成新状态节点),当它仍不是目标状态时,回溯到上一层结果,取另一可能扩展搜索的分支。采用相同办法一直进行下去,直到找到目标状态为止。
符合栈的先进后出(FILO)的性质。
具体过程:
1 每次取出栈顶元素,对其进行拓展。
2 若栈顶元素无法继续拓展,则将其从栈中弹出。继续1过程。
3 不断重复直到获得目标状态(取得可行解)或栈为空(无解)。
例一
输入n,输出能整除数字n的数字串,该串只有0,1两个数字构成。
#include<iostream>
#include<stdio.h>
using namespace std;
int n;
int flag=0;
void dfs(unsigned long long s ,int step ){
if(step>20||flag)return;
if(s % n == 0){
cout<<s<<endl;
flag = 1;
return;
}
dfs(s*10 , step+1);
dfs(s*10+1 , step+1);
}
int main(){
while(scanf("%d",&n)){
if(n==0)break;
flag=0;
dfs(1, 1);
}
return 0;
}