信息安全数学基础一

信息安全数学基础(一)
信息安全数学基础
——第一章 整数的可除性
文章目录
前言
本章讨论证书的算数性质、基本理论和方法,特别是整数、因数、素数、最大公因数、最小公倍数以及欧几里得除法和广义欧几里得除法,最后给出算数基本定理和素数定理。
提示:以下是本篇文章正文内容,下面案例可供参考,大多数都是自己整理的,适用于我自己,不一定适用于所有人。
一、整数的概念、欧几里得除法
1.1整除的概念
定义:设a、b是任意两个整数,其中b≠0.如果存在一个整数q使得等式a = q·b成立,就称b整除a或者a被b整除,记作b|a,并把b叫做a的因数,把a叫做b的倍数。
(1)整数传递性
定理:设a、b≠0,c≠0是三个整数,若b|a,c|b,则c|a.
例:因为7 | 42,42 | 84,所以7| 84
(2)加法运算
定理:设a、b、c≠0是三个整数,若c|a,c|b,则c|a±b
(3)整数的线性组合
定理:设a、b、c≠0是三个整数,若c|a,c|b,则对任意整数s、t,有c|(s·a+t·b)
(4)
定理:设a、b都是非零整数,若a|b,b|a,则a = ±b
(5)
定理:设n是一个正合数,p是n的一个大于1的最小正因数,则p一定是素数且p≤根号n
1.2Eratoshenes筛法(平凡除法)
定理:设n是一个正合数,如果对所有素数p≤根号n,都有p不能整除根号n,则n一定是素数
1.3欧几里得除法——最小非负余数
定理:设a、b是两个整数,其中b>0,则存在唯一的整数q,r使得a = q·b+r,0≤r<b.
1.4素数的平凡判别

1.5欧几里得除法——一般余数
定理:(欧几里得除法)设a、b是两个整数,其中b>0.则对任意的整数c,存在唯一的整数q,r使得a = q·b+r,c≤r<b+c.
二、最大公因数与广义欧几里得除法
2.1最大公因数
定理:设b是任一正整数,则(0,b)= b.
定理:设a,b,c是三个不全为零的整数.如果a = q·b+c,其中q是整数,则(a,b)=(b,c)
证明:设d=(a,b),d’=(b,c),则d|a,a|b.
∴ d | a+(-q)· b = c
∴ d是b,c的公因数
∴d≤d’
同理得到d’≤d
所以d=d’
定理成立
2.2广义欧几里得除法及计算最大公因数


2.3贝祖等式
定理:设a,b是任意两个正整数,则存在整数s,t使得s·a + t·b = (a,b).
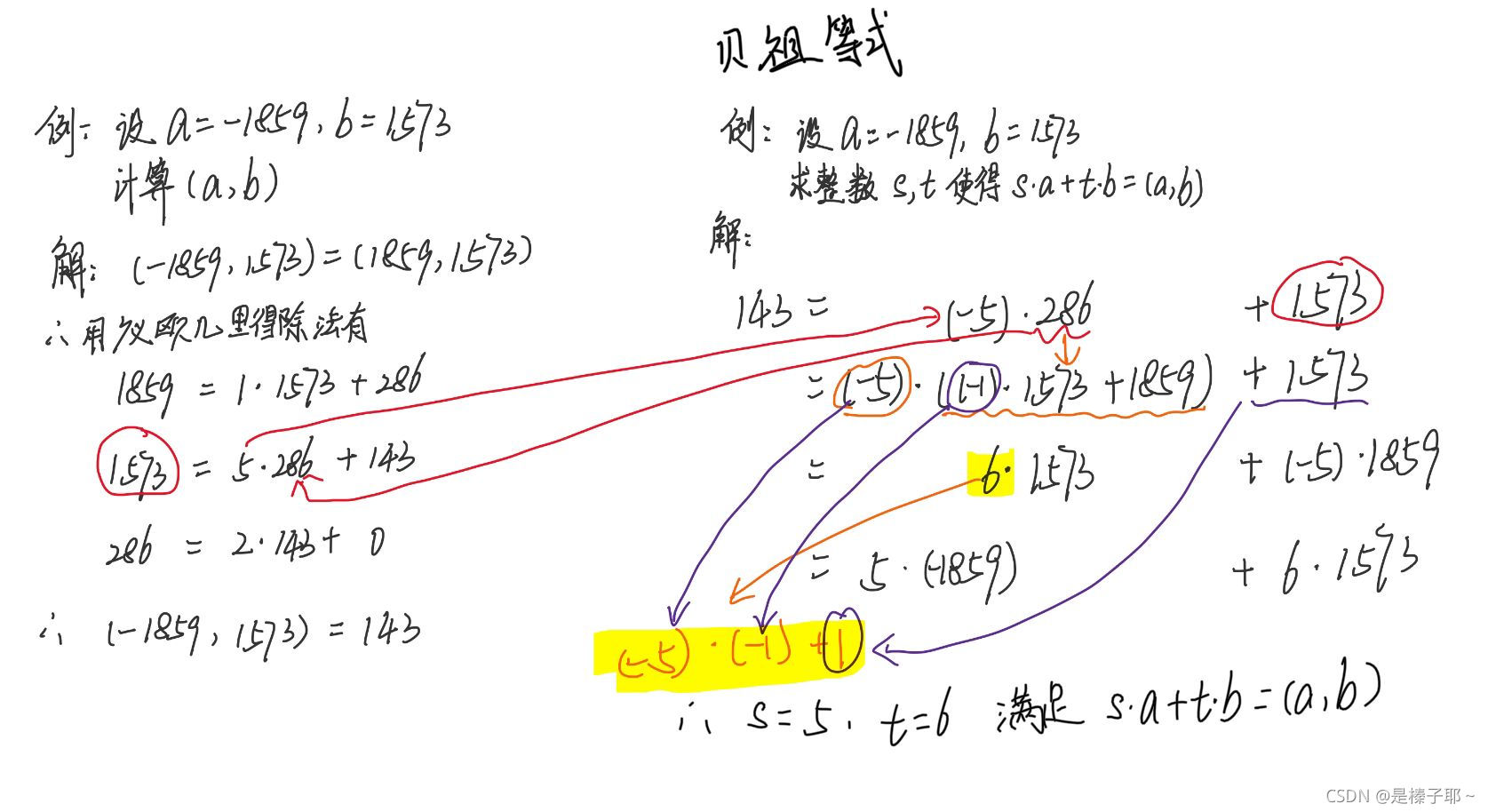
2.4 广义欧几里得除法
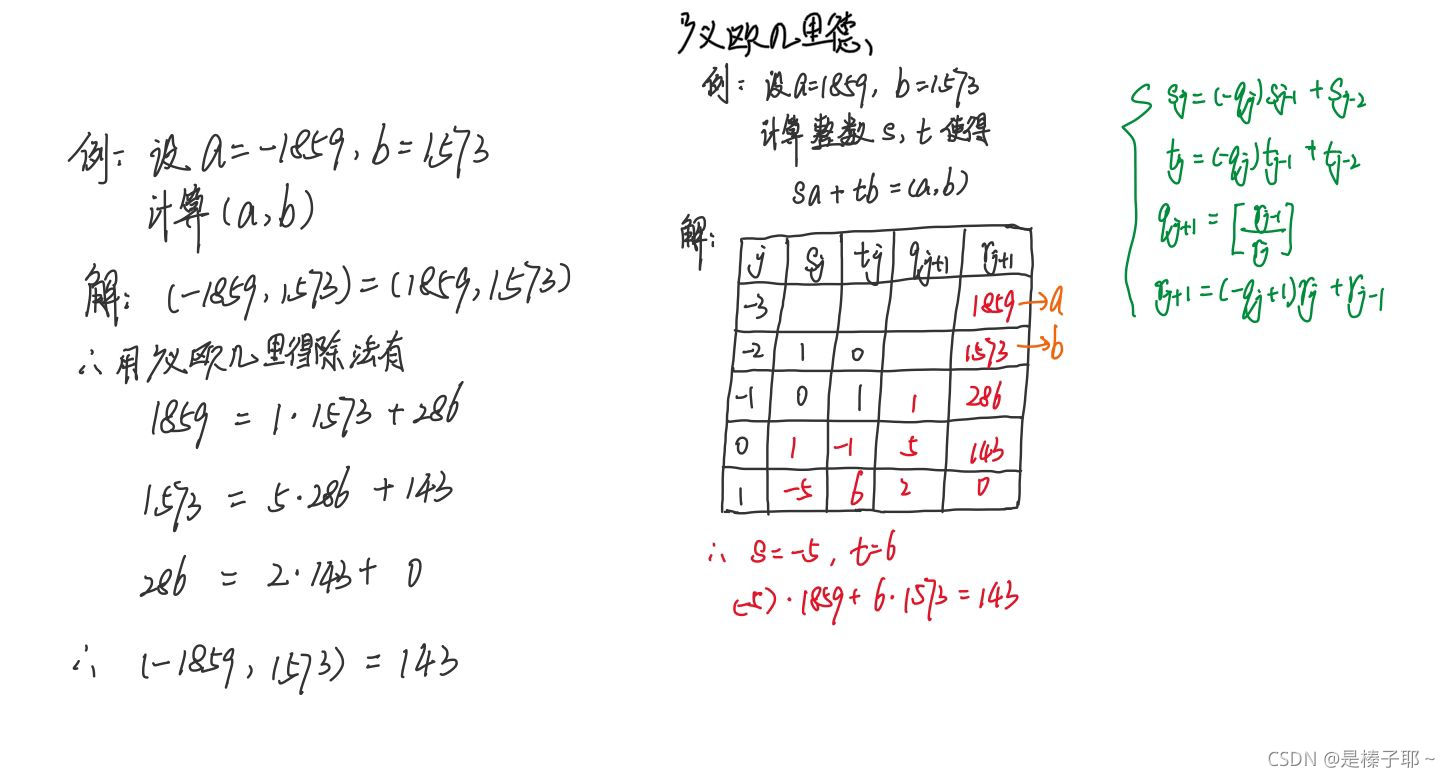
2.5多个整数的最大公因数及计算
定理:

例题:

2.6形为2^a - 1的整数及其最大公因数

三、整除的近一步性质及最小公倍数
3.1整数的进一步性质
定理:设a,b,c是三个整数,且c≠0.如果c|ab,(a,c)=1,则c|b.
定理:设p是素数,若p|ab,则p|a或p|b.
3.2最小公倍数
定理:设a,b是两个互素正整数,则(1)若a | D, b | D,则a·b | D;(2)[a,b] = a·b
3.3最小公倍数与最大公因数
定理:设a,b是两个正整数,则(1)若a | D, b | D,则[a,b] | D;
(2)[a,b]=a·b / (a,b)
3.4多个整数的最小公倍数
这里我直接上了例题,因为我觉得看例题比较好理解一些

四、习题
4.1证明:若2 | n,5 | n,7 | n,则70 | n.

4.2证明:如果a是整数,则a³-a被3整除.

4.3求最大公因数(55,85)

4.4广义欧几里得除法求整数s,t
(1613,3589)
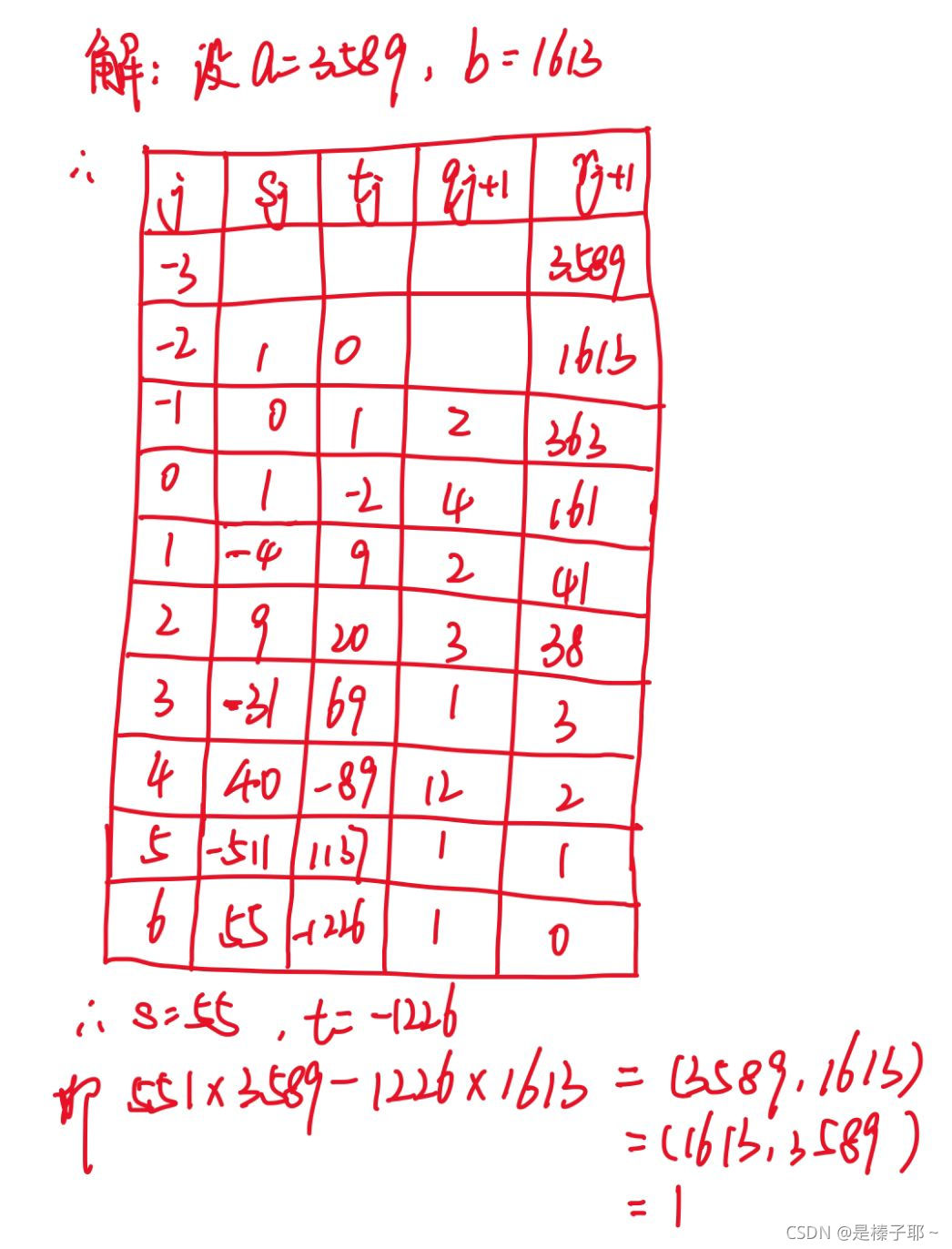
4.5证明:如果a,b,c是互素且非零的整数,那么(ab,c)= (a,b)(a,c)

4.6证明:若(a,4)=2,(b,4)=2,则(a+b,4)=4.

4.7求出下列各对数的最大公因数(a,b)及最小公倍数[a,b]
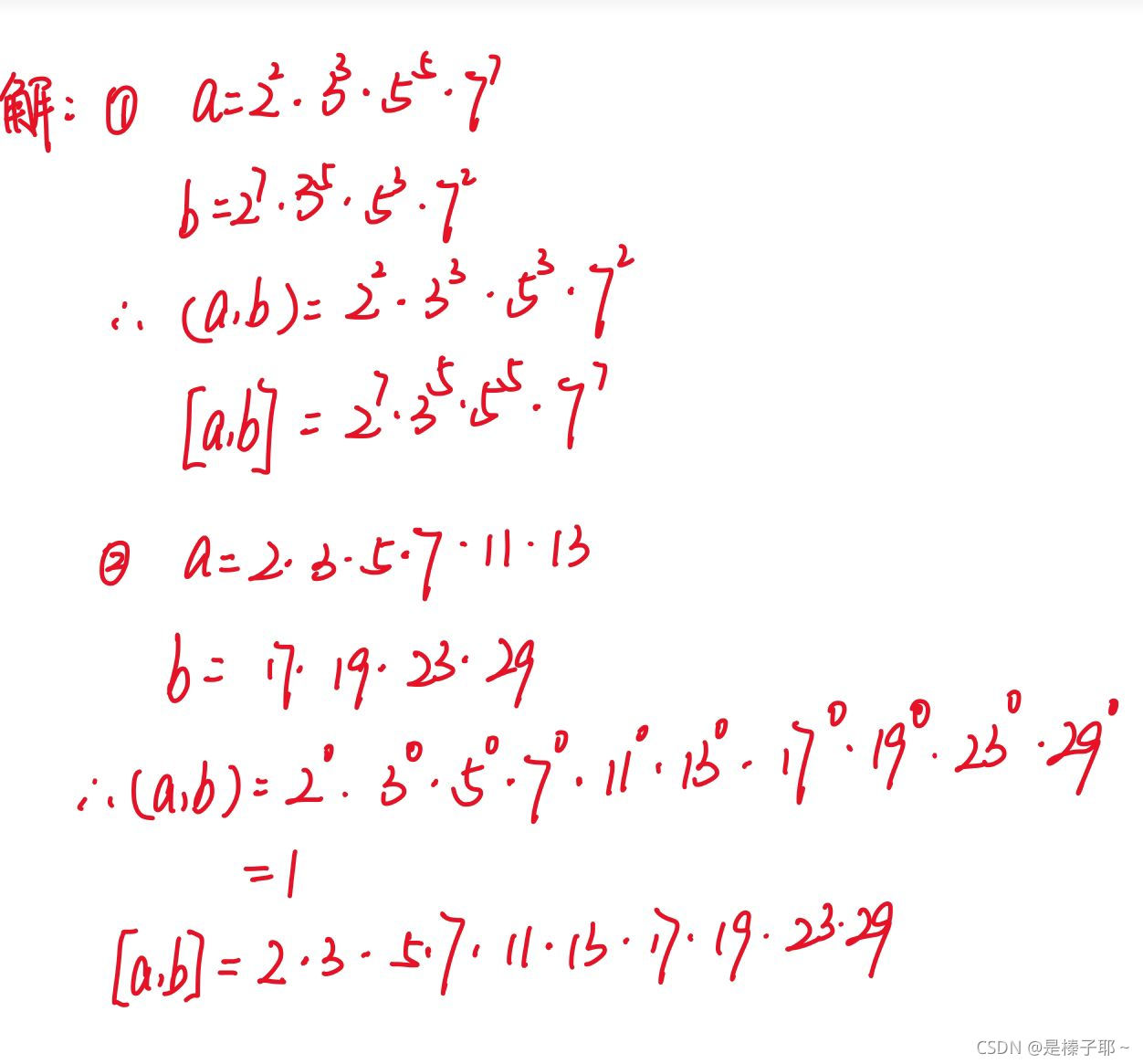
参考文献:《信息安全数学基础》第二版,陈恭亮