技术博客
首页 所有文章 标签 分类 关于
技术博客

目录

NAND-FLASH-三硬件ECC校验码详解

 收录于 Fpga
   约 2655 字   预计阅读 6 分钟 
https://bing.ee123.net/img/rand?artid=52104197

NAND FLASH （三）硬件ECC校验码详解

参考博客：

ECC的全称是Error Checking and Correction，是一种用于

Nand

的差错检测和修正算法。

如果操作时序和电路稳定性不存在问题的话，

NAND Flash

出错的时候一般不会造成整个

Block

或是

Page

不能读取或是全部出错，而是整个

Page

（例如

512Bytes

）中只有一个或几个

bit

出错。

ECC

能纠正

1

个

比特错误和检测2

个

比特错误，而且计算速度很快，但对

1

比特以上的错误无法纠正，对

2

比特以上的错误不保证能检测。

校验码生成算法：ECC

校验每次对

256

字节的数据进行操作，包含列校验和行校验。对每个待校验的

Bit

位求异或，若结果为

0

，则表明含有偶数个

1

；若结果为

1

，则表明含有奇数个

1

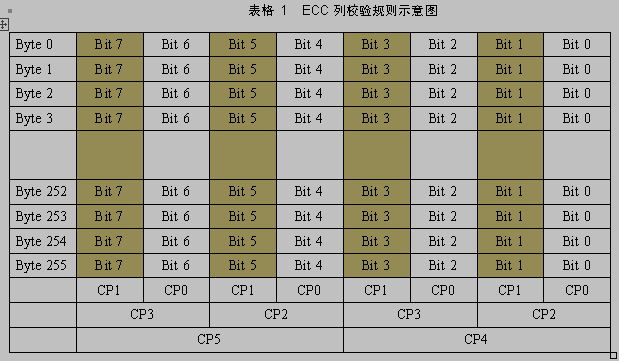
。列校验规则如表

1

所示。

256

字节数据形成

256

行、

8

列的矩阵，矩阵每个元素表示一个

Bit

位。

https://img-blog.csdn.net/20160803162753890

其中CP0 ~ CP5

为六个

Bit

位，表示

Column Parity

（列极性），

CP0

为第

0

、

2

、

4

、

6

列的极性，

CP1

为第

1

、

3

、

5

、

7

列的极性，

CP2

为第

0、

1

、

4

、

5

列的极性，

CP3

为第

2、

3

、

6

、

7

列的极性，

CP4

为第

0

、

1

、

2

、

3

列的极性，

CP5

为第

4

、

5

、

6

、

7

列的极性。

用公式表示就是：

CP0=

Bit0^Bit2^Bit4^Bit6， 表示第

0

列内部

256

个

Bit

位异或之后再跟第

2

列

256

个

Bit

位异或，再跟第

4

列、第

6

列的每个

Bit

位异或，这样，

CP0

其实是

256*4=1024

个

Bit

位异或的结果。

CP1 ~ CP5

依此类推。

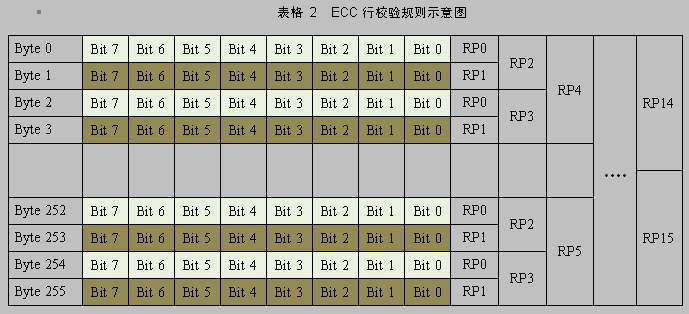
行校验如下图所示

https://img-blog.csdn.net/20160803163149940

其中RP0 ~ RP15

为十六个

Bit

位，表示

Row Parity

（行极性），

RP0

为第

0

、

2

、

4

、

6

、

….252、

254

个字节的极性

RP1—–1、

3

、

5

、

7

……253、

255

RP2—-0

、

1

、

4

、

5

、

8

、

9

…..252、

253

（处理

2

个

Byte

，跳过

2

个

Byte

）

RP3—- 2

、

3

、

6

、

7

、

10

、

11

…..254

、

255

（跳过

2

个

Byte

，处理

2

个

Byte

）

RP4—- 处理

4

个

Byte

，跳过

4

个

Byte

；

RP5—-

跳过

4

个

Byte

，处理

4

个

Byte

；

RP6—- 处理

8

个

Byte

，跳过

8

个

Byte

RP7—-

跳过

8

个

Byte

，处理

8

个

Byte

；

RP8—- 处理

16

个

Byte

，跳过

16

个

Byte

RP9—-

跳过

16

个

Byte

，处理

16

个

Byte

；

RP10—-处理

32

个

Byte

，跳过

32

个

Byte

RP11—-

跳过

32

个

Byte

，处理

32

个

Byte

；

RP12—-处理

64

个

Byte

，跳过

64

个

Byte

RP13—-

跳过

64

个

Byte

，处理

64

个

Byte

；

RP14—-处理

128

个

Byte

，跳过

128

个

Byte

RP15—-

跳过

128

个

Byte

，处理

128

个

Byte

；

可见，RP0 ~ RP15 每个

Bit

位都是

128

个字节（也就是

128

行）即

128*8=1024

个

Bit

位求异或的结果。

综上所述，对

256

字节的数据共生成了

6

个

Bit

的列校验结果，

16

个

Bit

的行校验结果，共

22

个

Bit

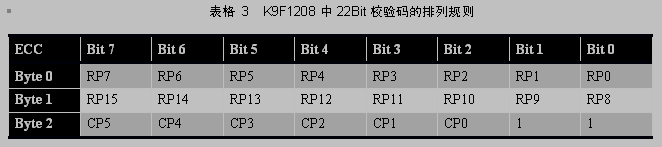
。在

Nand

中使用

3

个字节存放校验结果，多余的两个

Bit

位置

1

。存放次序如下表所示：

https://img-blog.csdn.net/20160803163516237

以

K9F1208

为例，每个

Page

页包含

512

字节的数据区和

16

字节的

OOB

区。前

256

字节数据生成

3

字节

ECC

校验码，后

256

字节数据生成

3

字节

ECC

校验码，共

6

字节

ECC

校验码存放在

OOB

区中，存放的位置为

OOB

区的第

0

、

1

、

2

和

3

、

6

、

7

字节。

校验码生成算法的 C

语言实现

在

Linux

内核中 ECC

校验算法所在的文件为

drivers/mtd/nand/nand_ecc.c

，其实现有新、旧两种，在

2.6.27

及更早的内核中使用的程序，从 2.6.28

开始已经不再使用，而换成了效率更高的程序。可以在

Documentation/mtd/nand_ecc.txt

文件中找到对新程序的详细介绍。

首先分析一下 2.6.27

内核中的

ECC

实现，源代码见

:

/*

  • Pre-calculated 256-way 1 byte column parity

*/

static const

[] = {

0x00, 0x55, 0x56, 0x03, 0x59, 0x0c, 0x0f, 0x5a, 0x5a, 0x0f, 0x0c, 0x59, 0x03, 0x56, 0x55, 0x00,

0x65, 0x30, 0x33, 0x66, 0x3c, 0x69, 0x6a, 0x3f, 0x3f, 0x6a, 0x69, 0x3c, 0x66, 0x33, 0x30, 0x65,

0x66, 0x33, 0x30, 0x65, 0x3f, 0x6a, 0x69, 0x3c, 0x3c, 0x69, 0x6a, 0x3f, 0x65, 0x30, 0x33, 0x66,

0x03, 0x56, 0x55, 0x00, 0x5a, 0x0f, 0x0c, 0x59, 0x59, 0x0c, 0x0f, 0x5a, 0x00, 0x55, 0x56, 0x03,

0x69, 0x3c, 0x3f, 0x6a, 0x30, 0x65, 0x66, 0x33, 0x33, 0x66, 0x65, 0x30, 0x6a, 0x3f, 0x3c, 0x69,

0x0c, 0x59, 0x5a, 0x0f, 0x55, 0x00, 0x03, 0x56, 0x56, 0x03, 0x00, 0x55, 0x0f, 0x5a, 0x59, 0x0c,

0x0f, 0x5a, 0x59, 0x0c, 0x56, 0x03, 0x00, 0x55, 0x55, 0x00, 0x03, 0x56, 0x0c, 0x59, 0x5a, 0x0f,

0x6a, 0x3f, 0x3c, 0x69, 0x33, 0x66, 0x65, 0x30, 0x30, 0x65, 0x66, 0x33, 0x69, 0x3c, 0x3f, 0x6a,

0x6a, 0x3f, 0x3c, 0x69, 0x33, 0x66, 0x65, 0x30, 0x30, 0x65, 0x66, 0x33, 0x69, 0x3c, 0x3f, 0x6a,

0x0f, 0x5a, 0x59, 0x0c, 0x56, 0x03, 0x00, 0x55, 0x55, 0x00, 0x03, 0x56, 0x0c, 0x59, 0x5a, 0x0f,

0x0c, 0x59, 0x5a, 0x0f, 0x55, 0x00, 0x03, 0x56, 0x56, 0x03, 0x00, 0x55, 0x0f, 0x5a, 0x59, 0x0c,

0x69, 0x3c, 0x3f, 0x6a, 0x30, 0x65, 0x66, 0x33, 0x33, 0x66, 0x65, 0x30, 0x6a, 0x3f, 0x3c, 0x69,

0x03, 0x56, 0x55, 0x00, 0x5a, 0x0f, 0x0c, 0x59, 0x59, 0x0c, 0x0f, 0x5a, 0x00, 0x55, 0x56, 0x03,

0x66, 0x33, 0x30, 0x65, 0x3f, 0x6a, 0x69, 0x3c, 0x3c, 0x69, 0x6a, 0x3f, 0x65, 0x30, 0x33, 0x66,

0x65, 0x30, 0x33, 0x66, 0x3c, 0x69, 0x6a, 0x3f, 0x3f, 0x6a, 0x69, 0x3c, 0x66, 0x33, 0x30, 0x65,

0x00, 0x55, 0x56, 0x03, 0x59, 0x0c, 0x0f, 0x5a, 0x5a, 0x0f, 0x0c, 0x59, 0x03, 0x56, 0x55, 0x00

};

为了加快计算速度，程序中使用了一个预先计算好的列极性表。这个表中每一个元素都是

unsigned char

类型，表示 8

位二进制数。

表中 8

位二进制数每位的含义：

https://img-blog.csdn.net/20160803164011803

这个表的意思是：对 0~255

这

256

个数，计算并存储每个数的列校验值和行校验值，以数作数组下标。比如

nand_ecc_

precalc_table[

13

]

存储 13

的列校验值和行校验值，

13

的二进制表示为

00001101

， 其

CP0 =

Bit0^Bit2^Bit4^Bit6

= 0 ；

CP1 = Bit1^Bit3^Bit5^Bit7 = 1 ；

CP2 = Bit0^Bit1^Bit4^Bit5 = 1;

CP3 = Bit2^Bit3^Bit6^Bit7 = 0;

CP4 = Bit0^Bit1^Bit2^Bit3 = 1;

CP5 = Bit4^Bit5^Bit6^Bit7 = 0;

其行极性 RP = Bit

0^Bit1

^

Bit2^

Bit3^

Bit4^

Bit5^

Bit6^

Bit7 =

1

；

则 nand_ecc_

precalc_table[

13

]

处存储的值应该是

0101 0110

，即 0x

注意，数组 nand_ecc_

precalc_table

的下标其实是我们要校验的一个字节数据。

理解了这个表的含义，也就很容易写个程序生成这个表了。程序见附件中的

MakeEccTable.c

文件。

有了这个表，对单字节数据 dat

，可以直接查表

nand_ecc_precalc_table[ dat ]

得到 dat

的行校验值和列校验值。 但是

ECC

实际要校验的是

256

字节的数据，需要进行

256

次查表，对得到的

256

个查表结果进行按位异或，最终结果的

Bit0 ~ Bit5

即是

256

字节数据的 CP0 ~ CP5.

/* Build up column parity */

for(

= 0;

< 256;

++) {

/* Get CP0 - CP5 from table */

=

[*

++];

^= (

& 0x3f);

//

这里省略了一些，后面会介绍

}

reg1

https://img-blog.csdn.net/20160803203452124

在这里，计算列极性的过程其实是先在一个字节数据的内部计算

CP0 ~ CP5,

每个字节都计算完后再与其它字节的计算结果求异或。而表 1

中是先对一列

Bit

0

求异或，再去异或一列

Bit2

。 这两种只是计算顺序不同，结果是一致的。 因为异或运算的顺序是可交换的。

行极性的计算要复杂一些。

nand_ecc_

precalc_table[]

表中的 Bit6

已经保存了每个单字节数的行极性值。对于待校验的

256

字节数据，分别查表，如果其行极性为

1

，则记录该数据所在的行索引（也就是

for

循环的

i

值），这里的行索引是很重要的，因为

RP

0 ~ RP15

的计算都是跟行索引紧密相关的，如 RP0

只计算偶数行，

RP1

只计算奇数行，等等。

ECC 纠错算法

当往 NAND Flash

的

page

中写入数据的时候，每

256

字节我们生成一个

ECC

校验和，称之为原

ECC

校验和，保存到

PAGE

的

OOB

（

out-of-band

）数据区中。

当从

NAND Flash

中读取数据的时候，每

256

字节我们生成一个

ECC

校验和，称之为新

ECC

校验和。

将从 OOB

区中读出的原

ECC

校验和新

ECC

校验和按位异或，若结果为

0

，则表示不存在错（或是出错了，

ECC

无法检测的错误）；若

3

个字节异或结果中存在

11

个比特位为

1

，表示存在一个比特错误，且可纠正；若

3

个字节异或结果中只存在

1

个比特位为

1

，表示

OOB

区出错；其他情况均表示出现了无法纠正的错误。

假设 ecc

_code_raw[3]

保存原始的 ECC

校验码，

ecc

_code_new[3]

保存新计算出的 ECC

校验码，其格式如下表所示：

https://img-blog.csdn.net/20160803210222612

对 ecc

_code_raw[3]

和 ecc_code_new

[3]

按位异或，得到的结果三个字节分别保存在

s0,s1,s2

中，如果 s

0s1s2

中共有 11

个

Bit

位为

1

，则表示出现了一个比特位错误，可以修正。定位出错的比特位的方法是，先确定行地址（即哪个字节出错），再确定列地址（即该字节中的哪一个

Bit

位出错）。

确定行地址的方法是：

设行地址为

unsigned char

byteoffs ，抽取

s1

中的

Bit7,Bit5,Bit3,Bit1

，作为 byte

offs

的高四位， 抽取

s

0 中的

Bit7,Bit5,Bit3,Bit1

作为

byteoffs

的低四位， 则

byteoffs

的值就表示出错字节的行地址（范围为 0 ~ 255

）。

确定列地址的方法是：

抽取

s2

中的

Bit7,Bit5,Bit3

作为 bitnum

的低三位，

bitnum

其余位置

0

，则

bitnum

的表示出错

Bit

位的列地址 （范围为

0 ~ 7

）。

参考博客的最后给举出了一个示例，可以帮助理解。

更新于 2025-01-31
 无标签
返回 | 主页