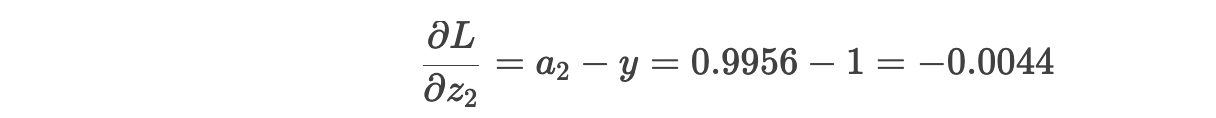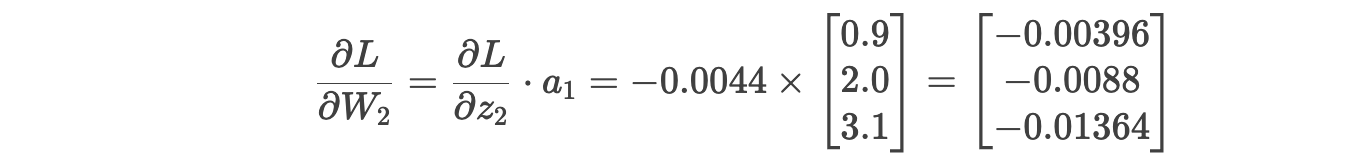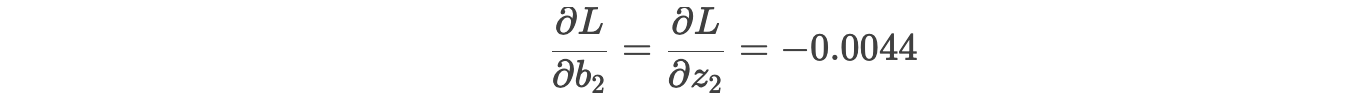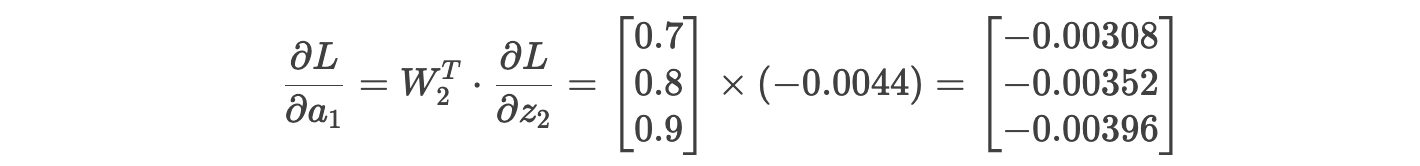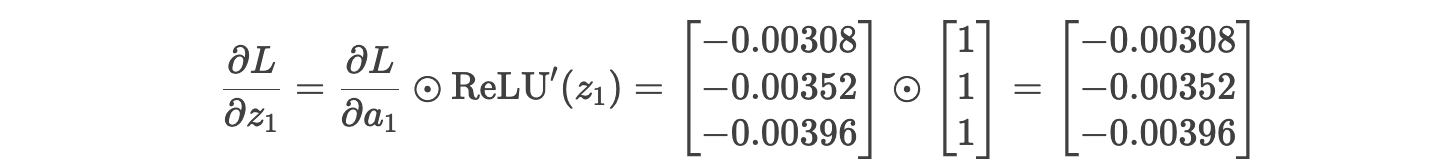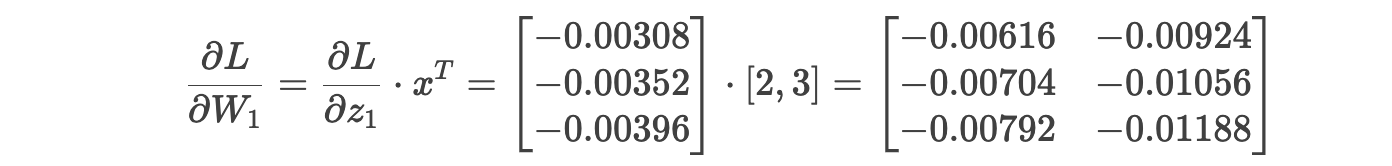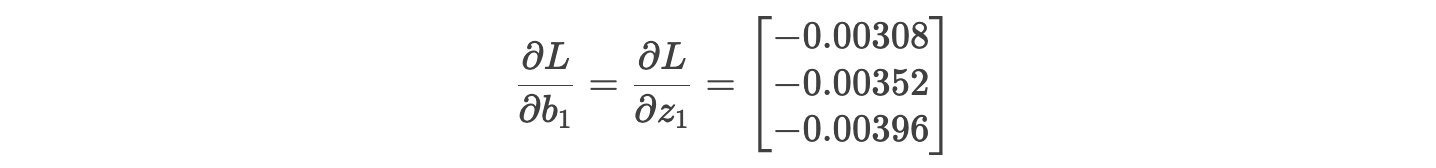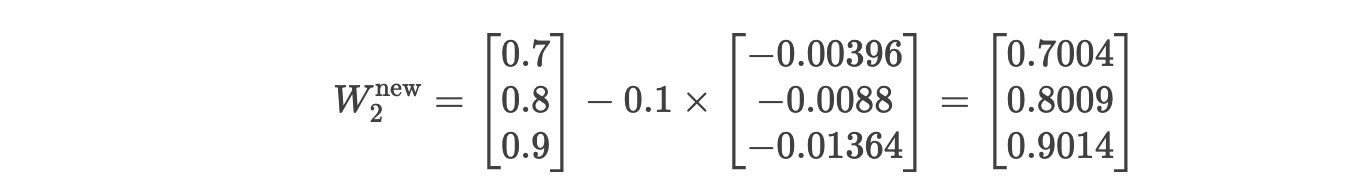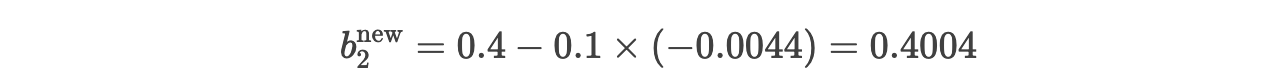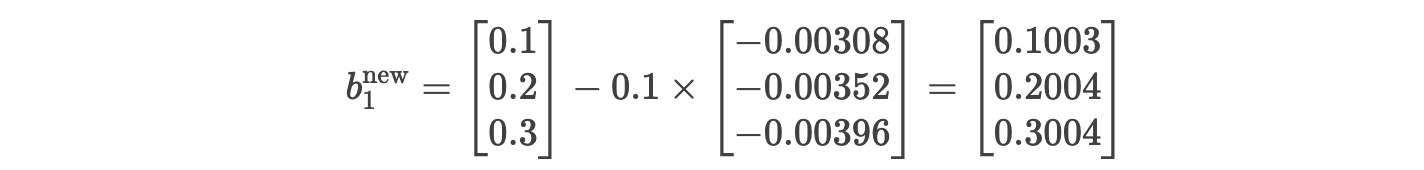前馈神经网络-参数学习梯度下降法-二分类任务

目录
前馈神经网络 - 参数学习(梯度下降法 - 二分类任务)
梯度下降法是训练前馈神经网络最常用的优化方法之一,其基本思想是:“根据当前参数下的损失函数的梯度信息,沿着使损失减小的方向更新参数,直到损失函数收敛到较低值(或满足停止条件)为止。”
本文中,基于二分类任务,我们来学习使用梯度下降法训练前馈神经网络。
以下通过一个具体的二分类任务,逐步展示梯度下降法如何调整神经网络参数。假设网络结构如下:
- 输入层 :2个神经元(特征 x1,x2)
- 隐藏层 :3个神经元(使用 ReLU 激活函数)
- 输出层 :1个神经元(使用 Sigmoid 激活函数)
1. 初始化参数
假设初始参数为:
输入层到隐藏层权重 W1 和偏置 b1:

隐藏层到输出层权重 W2 和偏置 b2:

2. 前向传播
输入样本 x=[2,3],真实标签 y=1。
步骤 2.1:计算隐藏层输入
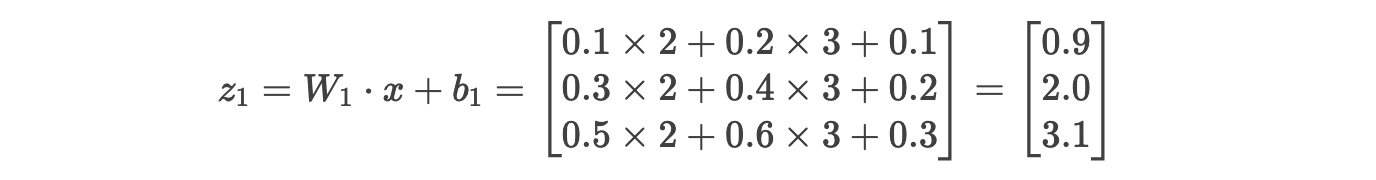
步骤 2.2:隐藏层激活(ReLU)
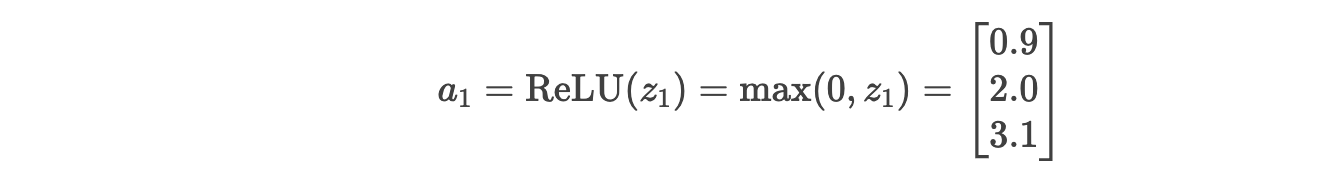
步骤 2.3:计算输出层输入
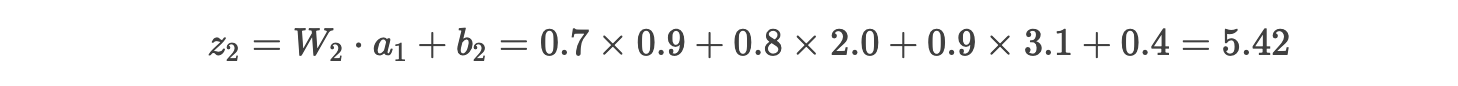
步骤 2.4:输出层激活(Sigmoid)
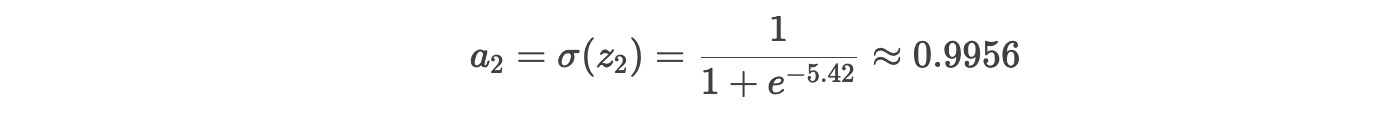
3. 计算损失
使用交叉熵损失函数:
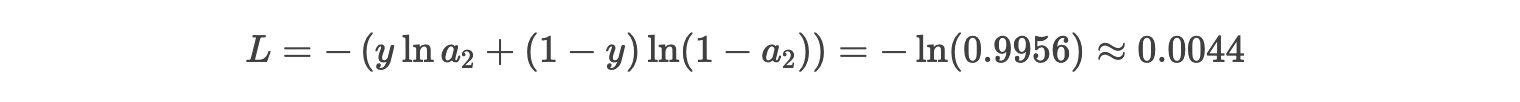
4. 反向传播(计算梯度)
目标:计算损失对每个参数(W1,b1,W2,b2)的梯度。
步骤 4.1:输出层梯度
损失对 z2 的导数 :

权重 W2 的梯度 :

偏置 b2 的梯度 :

步骤 4.2:隐藏层梯度
损失对 a1 的导数 :

损失对 z1 的导数 (ReLU导数为1,因为 z1>0):

权重 W1 的梯度 :

偏置 b1 的梯度 :

5. 参数更新(梯度下降法)
假设学习率 η=0.1,更新公式:
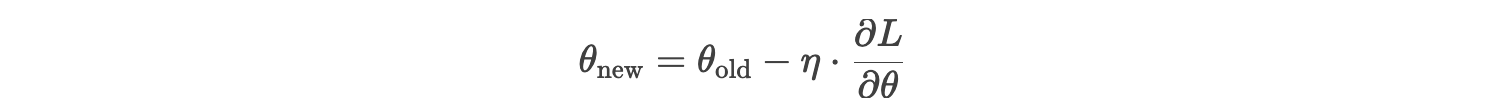
更新 W2 :

更新 b2 :

更新 W1 :

更新 b1 :

6. 迭代优化
重复以下步骤直至损失收敛:
- 前向传播 :计算当前参数下的预测值。
- 损失计算 :评估预测值与真实值的差距。
- 反向传播 :计算所有参数的梯度。
- 参数更新 :沿梯度负方向调整参数。
关键点总结
- 梯度计算 :通过链式法则从输出层反向传播至输入层。
- 矩阵维度对齐 :确保梯度矩阵与参数矩阵形状一致(如 ∂L∂W1∂W1∂L 应与 W1W1 同维度)。
- 学习率选择 :过大的学习率会导致震荡,过小则收敛缓慢。
- 批量训练 :实际应用中通常使用小批量样本(而非单个样本)计算梯度,以提高稳定性。
通过反复迭代,梯度下降法逐步调整参数,使神经网络的预测结果逼近真实值,最终完成模型训练。