蓝桥备赛（11）- 数据结构、算法与STL

一、数据结构

1.1 什么是数据结构？

**在计算机科学中，数据结构是一种 数据组织、管理和存储的格式 。它是相互之间存在

一种**

**或多种特定关系的数据元素的集合

。**

—>  通俗点，数据结构就是数据的组织形式 ， 研究数据是用什么方式存储在存储在g’v计算机中的

1.2 为什么会有数据结构？

1） 随着计算机的 发展和应用范围的拓展，计算机需要处理的数据量越来越大，数据类型越来越多， 数据之间的关系也越来越复杂 。

2）这就要求⼈们对计算机加工处理的数据进行系列的研究，即研究数据的特性、数据之间存在的关系，以及如何有效的组织、管理存储数据，

从而提高计算机处理数据的效率。

1.3 数据结构的三要素

1.3.1 逻辑结构

数据结构：数据中各元素之间的逻辑关系

他

只关心数据中各个元素之间的关系

， 并

不关心

数据在内存中存储的

1）集合： 所有数据只是放在一个集合中 ， 彼此之间再 没有 其他联系

2）线性结构：数据之间只存在一对一的关系

3）树：数据之间是一对多的关系

4）图结构：数据之间存在多对多的关系

1.3.2 存储结构

存储结构又称 物理结构 ， 但是存储二字 更能理解 ，后续我们统称为数据结构。

存储结构 顾名思义 ， 就是如何把数据在计算机中存储。

1） 顺序存储： 把逻辑上相邻的元素存储在  物理上也相邻的存储单元中  —> 数组（逻辑、物理上都是连续的）

**2）链式存储：

逻辑上两个元素相邻 ， 但是物理结构上不一定相邻**

1.3.3 数据的运算

数据的运算，（针对数据的各种操作） ， 包括 数据结构的实现 ， 以及基于数据结构上的各种操作。

—>   意思是 ， 我们已经知道 了一堆数据中  各个元素之间的关系 ， 也知道这堆数据应该在内存中如何存储 。

—-> 那么接下来就是写代码 ， 完成我们的需求

二、算法

2.1 什么是算法？

简单来说 —> 算法就是一系列的步骤 ， 用来将输入数据转化为输出结果（用来解决问题）

2.2 算法好坏的度量

算法设计好后，根据算法的设计原理，只要问题规模确定，算法中

基本语句执行次数 和 需求资源个数

基本也就确定了。

比如求

1 + 2 + 3 + … + (

n

− 1) +

n

，可以设计三种算法：

算法A ： 需要 开辟大小为N 的空间

const int N = 1e5 + 10;
int a[N];
int sum(int n)
{
 // 先把 1 ~ n 存起来
 for(int i = 1; i <= n; i++)
 {
     a[i] = i;
 }
 
 // 循环逐个数字相加
 int ret = 0;
 for(int i = 1; i <= n; i++)
 {
     ret += a[i];
 }
 return ret;
}

算法B：不需要开辟空间 ， 直接求和；

int sum(int n)
{
 // 循环逐个数字相加
 int ret = 0;
 for (int i = 1; i <= n; i++) 
 {
     ret += i;
 }
 return ret;
}

算法执行所需资源的个数与问题的规模 n 有关 。因此可以根据算法执行过程中对空间的消耗来衡量算法的好坏 ， 这就是 空间复杂度 。

算法C：需要循环 n 次 ， ret += n 语句会执行 n 次 ， 而且随着问题规模的增长 ， 执行次数也会增长 。

int sum(int n)
{
 int ret = 0;
 // 循环逐个数字相加
 for (int i = 1; i <= n; i++) 
 {
     ret += i;
 }
 return ret;
}

算法D ： 不管问题规模 n 为多少 ， ( 1 + n ) * n / 2 语句只会执行1次。

int sum(int n)
{
 // 利⽤求和公式
 return (1 + n) * n / 2;
}

算法中基本语句总的执行次数与问题规模 n 有关 。因此可以根据算法执行过程中 ， 所有语句被执行的次数之和来衡量算法的好坏 ， 这就是时间复杂度 。

综上所述 ， 时间和空间的消耗情况 就是我们 度量一个算法好坏的标准 ， 也就是时间复杂度和空间复杂度 。

2.3 时间复杂度

在计算机中 ， 算法的时间复杂度是一个函数式 T（N） ， 他定量描述了该算法的运行时间 。这个T（N）函数式 计算了程序中语句的执行次数 。

计算一下 fun 中++count 语句总共执行了多少次 。

void fun(int N) 
{ 
 int count = 0; 
 for(int i = 0; i < N; i++) 
 { 
     for(int j = 0; j < N; j++) 
     { 
         ++count; // 执⾏次数是 n*n，也就是 n^2
     } 
 } 
 for(int k = 0; k < 2 * N; k++) 
 {
     ++count; // 执⾏次数是 2*n
 } 
 
 int M = 10; 
 while(M--) 
 { 
     ++count; // 执⾏次数 10
 } 
}

2.3.1 大O表示法

因此，在计算时间复杂度的时候，一

般会把中对结果影响不大的项忽略掉

，这种表示时间复杂度的方式称

为大 O 渐进时间复杂度 - 粗略的估计方式

， 只看影响时间开销最大的⼀项。

2.3.2 最优、平均和最差时间复杂度

案例：在

n

个整形元素数组中，检测

x

是否存在，若存在返回其在数组中的下标，否则返回

−1

。

int find (int a[], int n, int x)
{
 for (int i = 0; i < n; i++)
 {
     if (a[i] == x) 
     return i;
 }
     return -1;
}

1） 在查找过程中，

x 与数组中元素依次比较，

因此总的比较次数就是该算法的时间复杂度。

—>   若待查找元素

x

为

21

，只需要比较

1

次，为算法的 最优(好)情况 。

—>   若带查找元素

x

为

17 ，或者是不存在的元素，需要比较 n 次，为算法的 最坏(差)情况 。

—>   所有情况的比较 次数之和，除以总情况，为 算法的平均情况。

无论是在竞赛还是工程中，算法的时间复杂度⼀般为最差情况。

因为最差情况是人对⼀件事情所能承受的底线

， 因此 find **算法的时间复杂度为

O

(

n**

)

。

2.3.3 时间复杂度计算案例

案例一：

案例二：

基本语句

++count

关于问题规模

n

总执行次数的数学表达式为:

f

(

n

) = 1000

；

不论

n

如何变化，

++count 总的执行次数都是

1000

， 故时间复杂度为： **O

(1)

。**

案例三：

void func3(int m, int n)
{
     for (int i = 0; i < m; i++)
     {
     printf("hello\n");
     }
 
     for (int i = 0; i < n; i++)
     {
     printf("hello\n");
     }
}

基本语句 printf("") 总的执行次数为 f ( m , n ) = m + n ；

m 和 n 的变化都是影响基本语句执行次数，

即m  和 n 都是问题规模，

故时间复杂度为

O

(

m

n

)

，

或者也可以表示为 O ( max（m,n)) 。

案例四：

基本语句 printf("") 总的执行次数为 f ( m , n ) = m x n ；

m 和 n 的变化都是影响基本语句执行次数，

即m  和 n 都是问题规模，

故时间复杂度为

O

(

m x

n

)

案例5：

void func5(int n)
{
     int cnt = 1;
     while (cnt < n)
     {
     cnt *= 2;
     }
}

案例六：

递归算法时间复杂度求解方式为，单次递归时间 × 总的递归次数。

注意，这里只是简易的估算方式。递归算法的时间复杂度严谨的计算方法是

利用主定理

(Master Theorem)来求得递归算法的时间复杂度

。

O( n )

2.4 空间复杂度

在算法竞赛中，空间复杂度就是整个程序在解决这个问题时，

⼀共使用了多少空间。相比较于时间复杂度，空间复杂度就没那么受关注，因为多数情况下题目所给的内存限制是非常宽裕的。

但是，这并不表明可以肆无忌惮的使用空间，一旦超出给定的限制，程序也是不会通过的。 - MLE

案例一：冒泡排序

#include <iostream>
using namespace std;

const int N = 20;
int arr[N];

int main()
 {
	int n = 0;
	cin >> n;
	int i = 0;
 	//输入 
	 for(i=0; i < n; i++)
	 	cin >> arr[i];
	 //排序
	 for(i = 0; i < n-1; i++)
	 {
		 int j = 0;
		 for(j = 0; j <= n-1-i; j++)
		 {
			if(arr[j] < arr[j+1])
			 {
				 int tmp = arr[j];
				 arr[j] = arr[j+1];
				 arr[j+1] = tmp; 
			 }
		 }
	 } 
	 //输出
	for(i=0; i < n; i++)
	{
		cout << arr[i] << endl;
	}
 	return 0;
 }

案例二：递归求阶乘

2.5 常见复杂度的增长对比

2.6 算法中的时间和空间限制

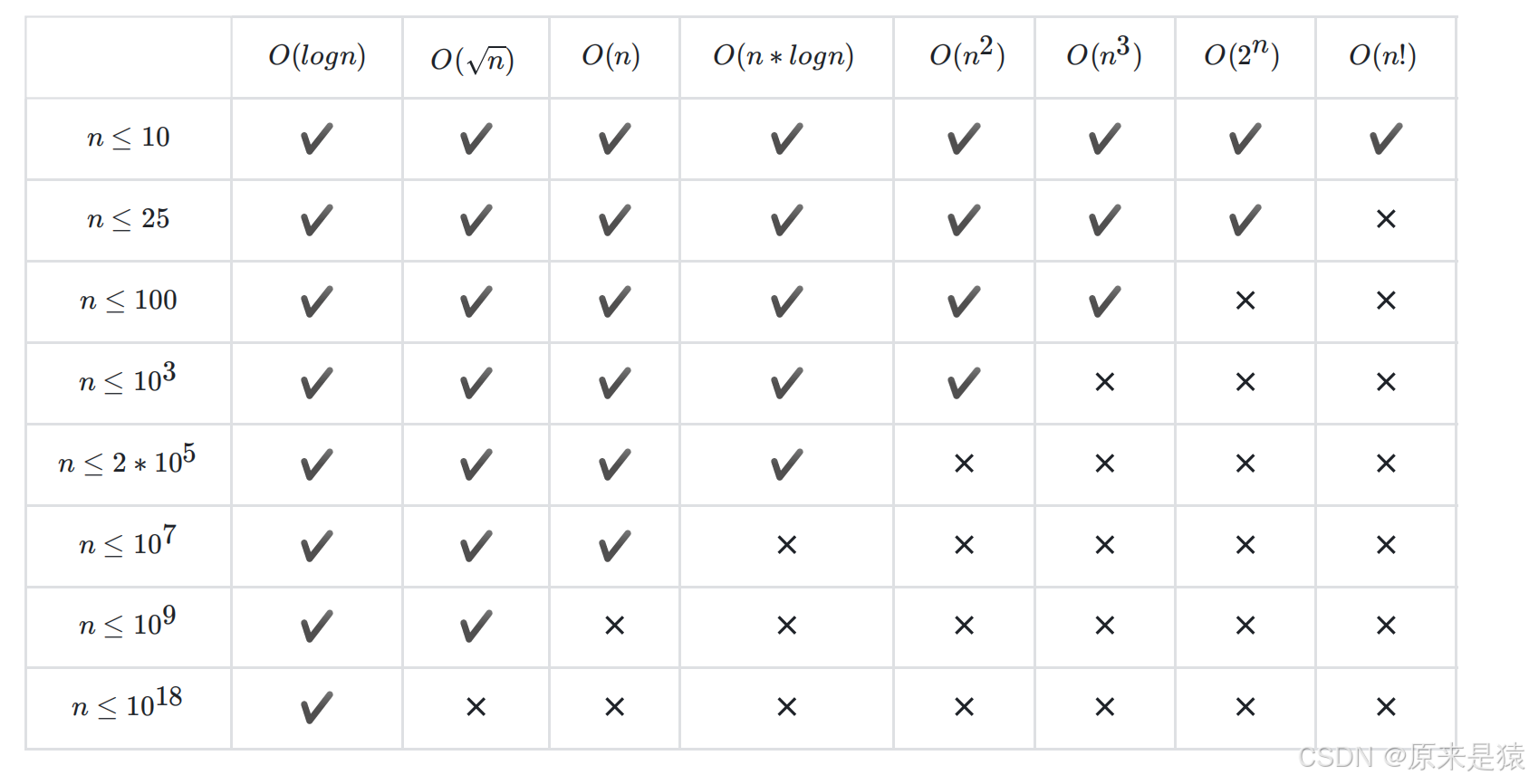
1. 信息学竞赛中，C++ 通常设定 1 到 2 秒的时间限制，运行次数在 10^7 ⾄ 10^8 之间。

2.空间限制在128MB 或 256MB ，可以开⼀个3 x 10 ^7 大小的int  类型数组，或者5000x5000大小的二维数组，⼀般情况下都是够⽤的。

各种数据量下，可选用的算法的时间复杂度：

三、STL

3.1 C++标准库

1） C++标准是C++编程语言的规范，由国际标准化组织（ISO）制定。C++标准的发展历程可以追溯到 1998年，当时ISO/IEC 14882:1998标准被发布，这是第⼀个C++标准，常被称为C++98。随后，C++标准经历了多次更新和修订，包括C++03（2003年）、C++11（2011年）、C++14（2014年）、C++17（2017年）以及 C++20。

2）最新的C++标准是C++23，于2023年发布，引入了许多新特性，

但目前完整的编译器较少。

3）每⼀个版本的 C++ 标准不仅规定了 C++ 的语法、语言特性，还规定了⼀套 C++ 内置库的实现规范，这个库便是 C++ 标准库。C++ 标准库中包含大量常用代码的实现，如输入输出、基本数据结构、内存管理、多线程支持等。

4） 我们可以这样简单的理解，C++ 给我们提供了一大堆的代码，这些代码里面包含特别多已经实现好的

数据结构 和 算法 。

因此，在做题的时候，如果涉及的数据结构和算法 C++ 标准库已经帮我们实现好

了，那么就可以直接使用，避免重复造轮子

。

— sort / min / max / swap

1） 造轮子指的是重复发明已有的算法，或者重复编写现成优化过的代码。

2）造轮子通常耗时好力，同时效果还没有别人好。但若是为了学习或者练习，造轮子则是必要的。

因此，学好 C++ 标准库能极大的提高编程效率。

3.2 什么是STL？

STL 即标准模板库（Standard Template Library） ，是 C++ 标准库的一部分，

里面包含了⼀些模板化的通过用的数据结构和算法

。由于其模板化的特点，它能够兼容自定义的数据类型，避免大量的造轮子工作。

NOI 和 ICPC 赛事都支持 STL 库的使用，当然，

蓝桥杯也是支持的

。因此，⼀定要学习 STL 的使用，

能够极大的提高编写代码的效率。

3.3 怎么学习STL？

模范使用！！！

STL 的实现涉及比较⾼深的 C++ 知识，

比如类、模板、容器适配器等

。如果想 搞清楚背后的原理，就必须要学会这些知识。但是这些知识在竞赛中是用不到的，如果深究，会浪费

大量无用的时间。 因此，目前先把重点放在如何使用上 。