大模型系列一适合初学者的深度学习入门2

大模型系列(一)——适合初学者的深度学习入门(2)
2.3 反向传播
在 中讲述了前向传播算法的过程是输入经过连续的矩阵相乘和激活函数得到输出,而连续相乘的矩阵就是权重(weight),其初始化是通过随机初始化完成的,那么将输入与之相乘得到的结果与真实值必然有所偏差,那么如何能得到最终的权重,使得输入得到与真实值相近的输出,就是训练神经网络的目的。这个方法就是梯度下降算法。
2.3.1 梯度下降算法
梯度下降算法是怎么工作的呢?
θ :
θ − α ∇ θ J ( θ ) \theta := \theta - \alpha \nabla_\theta J(\theta)
θ
:=
θ
−
α
∇
θ
J
(
θ
)
式子很简单,表示
θ \theta
θ 更新之后的值为当前值减去学习率
× \times
× 当前值的导数值,先看一个二次函数的例子,在高中的时候我们就已经学会使用导数求形如
f ( x )
a x 2 + b x + c , ( a
0 ) f(x)=ax^2+bx+c,;(a>0)
f
(
x
)
=
a
x
2
b
x
c
,
(
a
0
) 这样的二次函数的最小值了,当导数为0的时候就是最小值对应的
x x
x 。
在神经网络中,我们通常用均方误差(MSE)来表示输出和真实值之间的误差:
MSE
1 2 n ∑ i
1 n ( y i − y ^ i ) 2 \text{MSE} = \frac{1}{2n} \sum_{i=1}^{n} (y_i - \hat{y}_i)^2
MSE
=
2
n
1
i
=
1
∑
n
(
y
i
−
y
^
i
)
2
这个式子表达的意思是,每一个输出的所有维度
y i y_i
y
i
跟对应的真实值的维度
y ^ i \hat{y}_i
y
^
i
取差值的平方,再将求出的平方求和,这就是一个样本的取差值,再将所有参与训练的样本(个数为
n n
n )求和取平均值就是所有样本相对于真实值的误差值。显而易见,这个数肯定是越小越好,训练神经网络的目的就是找到合适的权重使得MSE尽量的小,也就是我们要求取使得MSE最小的
W W
W 。但是问题是
W W
W 是许多的矩阵,要求导一定涉及到偏导数,并且也很难找到导数为0的那个点,而且我们采用的是随机数初始化权重,谁也不能保证初始化的
W W
W 落在哪里。类比一下二次函数,可能初始化就落在下图中的
x
7.5 x=7.5
x
=
7.5 的位置了,在神经网络中只能摸索着找到最低点,而某一个点的梯度实际上就是沿着曲线下降最快的方向,因此沿着这条线可以以最快的速度接近最小值,而上文中提到的
α \alpha
α 学习率就是控制一步走多大的,那么随着向最值点移动,梯度也越来越小,学习率不变的情况下就会逐渐趋近与最值点。
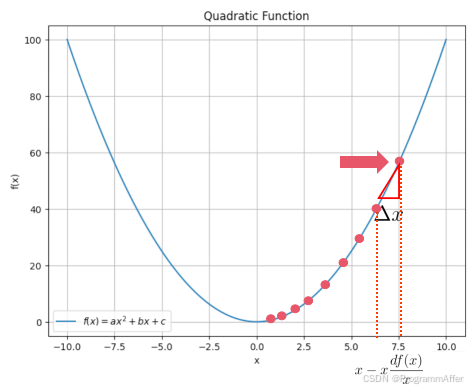
当迭代到一定次数或者两次迭代之间
x x
x 的差值小于百分之多少的时候就可以停止迭代,认为当前的
x x
x 就是极值点了。在神经网络的训练中也是采用相同的方式,只不过神经网络中需要更新权重矩阵中的数值,并且浅层网络和深层网络的权重都需要更新,那么最终的误差值的梯度是如何传导给浅层网络的呢?这就是接下来的反向传播算法。
2.3.2 反向传播算法详解
上一节说了神经网络的训练方法——梯度下降法,就是摸索着从一个随机初始点开始,每次迭代减去学习率
× \times
× 当前值的导数,就可以逐渐找到使得误差函数最小的极值点,那么针对下图的神经网络,每一次隐藏层的传递都是一个权重矩阵,这些权重矩阵的误差值该如何计算?也就是说输出端的误差是如何传递给前面
W 1 \boldsymbol{W_1}
W
1
、
W 2 \boldsymbol{W_2}
W
2
以及
W 3 \boldsymbol{W_3}
W
3
的?
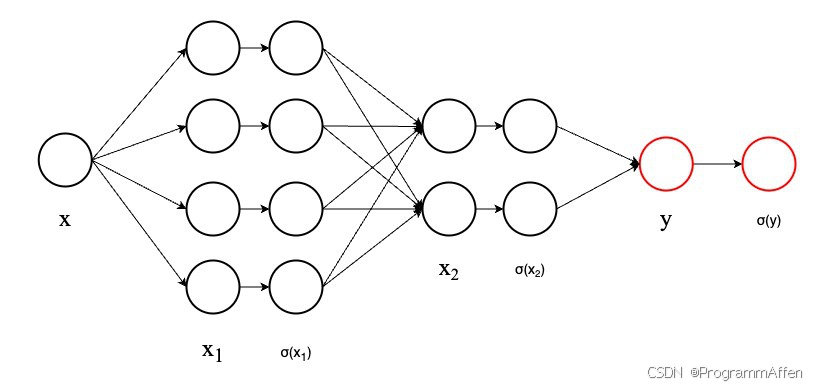
x 1
W 1 x + b 1 σ ( x 1 )
l e a k y _ R e l u ( x 1 ) x 2
W 2 σ ( x 1 ) + b 2 σ ( x 2 )
l e a k y _ R e l u ( x 2 ) y
W 3 σ ( x 2 ) + b 3 σ ( y )
l e a k y _ R e l u ( y ) \boldsymbol{x_1} = \boldsymbol{W_1}\boldsymbol{x} + \boldsymbol{b_1} \ \boldsymbol{\sigma(x_1)} = leaky_Relu(\boldsymbol{x_1}) \ \boldsymbol{x_2} = \boldsymbol{W_2}\boldsymbol{\sigma(x_1)} + \boldsymbol{b_2} \ \boldsymbol{\sigma(x_2)} = leaky_Relu(\boldsymbol{x_2}) \ \boldsymbol{y} = \boldsymbol{W_3}\boldsymbol{\sigma(x_2)} + \boldsymbol{b_3} \ \boldsymbol{\sigma(y)} = leaky_Relu(\boldsymbol{y})
x
1
=
W
1
x
b
1
σ
(
x
1
)
=
l
e
ak
y
_
R
e
l
u
(
x
1
)
x
2
=
W
2
σ
(
x
1
)
b
2
σ
(
x
2
)
=
l
e
ak
y
_
R
e
l
u
(
x
2
)
y
=
W
3
σ
(
x
2
)
b
3
σ
(
y
)
=
l
e
ak
y
_
R
e
l
u
(
y
)
首先要知道导数的链式法则,因为导数是一层层从输出层向输入层传导的。如果有
h ( x )
f ( g ( x ) ) h(x)=f(g(x))
h
(
x
)
=
f
(
g
(
x
)) ,那么复合函数的导数
h ′ ( x ) h’(x)
h
′
(
x
) 为:
h ′ ( x )
f ′ ( g ( x ) ) ⋅ g ′ ( x ) h’(x) = f’(g(x)) \cdot g’(x)
h
′
(
x
)
=
f
′
(
g
(
x
))
⋅
g
′
(
x
)
接着我们一步一步来,尽量减少用复杂的上下标表示矩阵的各个位置,对于初学者来说很不友好。
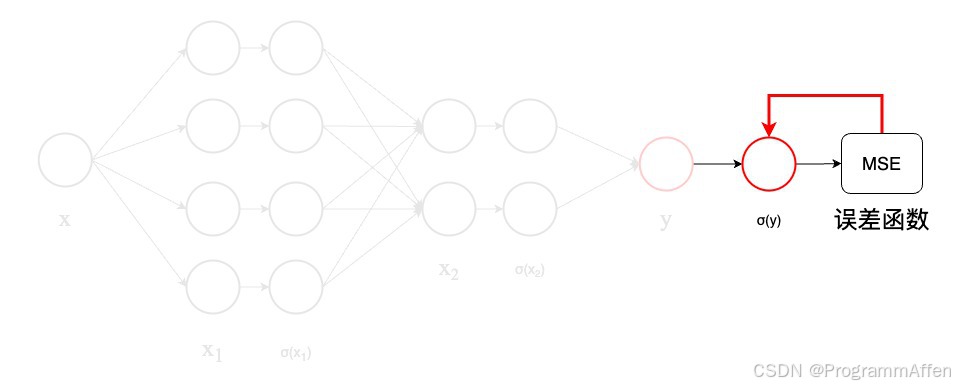
**1)误差函数对
σ ( y ) \boldsymbol{\sigma}(\boldsymbol{y})
σ
(
y
) 的求导:**
d ( MSE ) d σ ( y )
1 n ∑ i
1 n ( σ ( y i ) − y ^ i ) \frac{d(\text{MSE})}{d\sigma(y)} = \frac{1}{n} \sum_{i=1}^{n} (\sigma(y_i) - \hat{y}_i)
d
σ
(
y
)
d
(
MSE
)
=
n
1
i
=
1
∑
n
(
σ
(
y
i
)
−
y
^
i
)
以上其实就是二次函数的求导,这样看可能不太直观,我们举一个输出有3个特征的例子,最终的输出为
[ y 1 , y 2 , y 3 ] T [y_1,y_2,y_3]^T
[
y
1
,
y
2
,
y
3
]
T ,而真实值为
[ y 1 ^ , y 2 ^ , y 3 ^ ] T [\hat{y_1},\hat{y_2},\hat{y_3}]^T
[
y
1
^
,
y
2
^
,
y
3
^
]
T ,那么最终的误差函数为:
MSE
1 2 ( ( y 1 − y ^ 1 ) 2 + ( y 2 − y ^ 2 ) 2 + ( y 3 − y ^ 3 ) 2 ) \text{MSE} = \frac{1}{2} ((y_1 - \hat{y}_1)^2 + (y_2 - \hat{y}_2)^2 + (y_3 - \hat{y}_3)^2)
MSE
=
2
1
((
y
1
−
y
^
1
)
2
(
y
2
−
y
^
2
)
2
(
y
3
−
y
^
3
)
2
)
由于有3个特征,那么需要误差函数对三个特征求偏导数:
d ( M S E ) d y
[ ∂ ( M S E ) ∂ y 1 ∂ ( M S E ) ∂ y 2 ∂ ( M S E ) ∂ y 3 ]
[ y 1 − y 1 ^ y 2 − y 2 ^ y 3 − y 3 ^ ] \frac{d(MSE)}{dy} = \begin{bmatrix} \frac{\partial (MSE)}{\partial y_1} \ \frac{\partial(MSE)}{\partial y_2} \ \frac{\partial(MSE)}{\partial y_3} \ \end{bmatrix} = \begin{bmatrix} y_1 - \hat{y_1} \ y_2 - \hat{y_2} \ y_3 - \hat{y_3}\ \end{bmatrix}
d
y
d
(
MSE
)
=
∂
y
1
∂
(
MSE
)
∂
y
2
∂
(
MSE
)
∂
y
3
∂
(
MSE
)
=
y
1
−
y
1
^
y
2
−
y
2
^
y
3
−
y
3
^
如果有
n n
n 个样本的话,误差函数对输出的导数就变为:
d ( M S E ) d y
[ 1 n ∑ i
1 n y 1 − y 1 i ^ 1 n ∑ i
1 n y 2 − y 2 i ^ 1 n ∑ i
1 n y 3 − y 3 i ^ ] \frac{d(MSE)}{dy} = \begin{bmatrix} \frac{1}{n} \sum_{i=1}^{n} y_1 - \hat{y_1^i} \ \frac{1}{n} \sum_{i=1}^{n} y_2 - \hat{y_2^i} \ \frac{1}{n} \sum_{i=1}^{n} y_3 - \hat{y_3^i}\ \end{bmatrix}
d
y
d
(
MSE
)
=
n
1
∑
i
=
1
n
y
1
−
y
1
i
^
n
1
∑
i
=
1
n
y
2
−
y
2
i
^
n
1
∑
i
=
1
n
y
3
−
y
3
i
^
实际上就是把所有的样本针对每一个特征的导数求一个平均值,到这里就完成了误差函数对输出的求导,求导完的矩阵与输出的维度相同。而我们举的二次函数的例子输出和导数都只有1个维度。
**2)激活函数
σ ( y ) \boldsymbol{\sigma}(\boldsymbol{y})
σ
(
y
) 对
y \boldsymbol{y}
y 的求导:**
激活函数的导数非常简单:
d σ ( y ) y
{ 1 , if y ≥ 0 α , if y < 0 \frac{d\sigma(y)}{y} = \begin{cases} 1, & \text{if } y \geq 0 \ \alpha, & \text{if } y < 0 \end{cases}
y
d
σ
(
y
)
=
{
1
,
α
,
if
y
≥
0
if
y
<
0
根据导数的链式传导规则,误差函数对
y y
y 的导数为:
d ( M S E ) d y
d ( M S E ) d σ ( y ) ⋅ d σ ( y ) d y \frac{d(MSE)}{dy} = \frac{d(MSE)}{d\sigma(y)} \cdot \frac{d\sigma(y)}{dy}
d
y
d
(
MSE
)
=
d
σ
(
y
)
d
(
MSE
)
⋅
d
y
d
σ
(
y
)
如果还是以刚才三个特征的
y y
y 举例子(假设
y 1 < 0 y_1<0
y
1
<
0 ,
y 2 , y 3
0 y_2,y_3>0
y
2
,
y
3
0 ):
d ( M S E ) d y
[ 1 n ⋅ α ⋅ ∑ i
1 n y 1 − y 1 i ^ 1 n ⋅ 1 ⋅ ∑ i
1 n y 2 − y 2 i ^ 1 n ⋅ 1 ⋅ ∑ i
1 n y 3 − y 3 i ^ ] \frac{d(MSE)}{dy} = \begin{bmatrix} \frac{1}{n} \cdot \alpha \cdot \sum_{i=1}^{n} y_1 - \hat{y_1^i} \ \frac{1}{n} \cdot 1 \cdot \sum_{i=1}^{n} y_2 - \hat{y_2^i} \ \frac{1}{n} \cdot 1 \cdot \sum_{i=1}^{n} y_3 - \hat{y_3^i}\ \end{bmatrix}
d
y
d
(
MSE
)
=
n
1
⋅
α
⋅
∑
i
=
1
n
y
1
−
y
1
i
^
n
1
⋅
1
⋅
∑
i
=
1
n
y
2
−
y
2
i
^
n
1
⋅
1
⋅
∑
i
=
1
n
y
3
−
y
3
i
^
此时就完成了激活函数对
y y
y 的求导:
注意:
上面用含有3个特征的y进行举例只是为了说明从误差函数到激活函数到y求导的过程中维度没有发生变化,在当前我们举的二次函数的例子中,因为输出维度是1有一定特殊性,所以才举了3个特征的例子来说明。
3) **y \boldsymbol{y}
y 对
W \boldsymbol{W}
W 和
b \boldsymbol{b}
b 的误差:**
这一步骤非常非常关键,我们前面费了这么大劲将误差的梯度传导到这里就是为了求误差函数对于
W \boldsymbol{W}
W 和
b \boldsymbol{b}
b 的导数从而可以使得其进行梯度下降的计算。
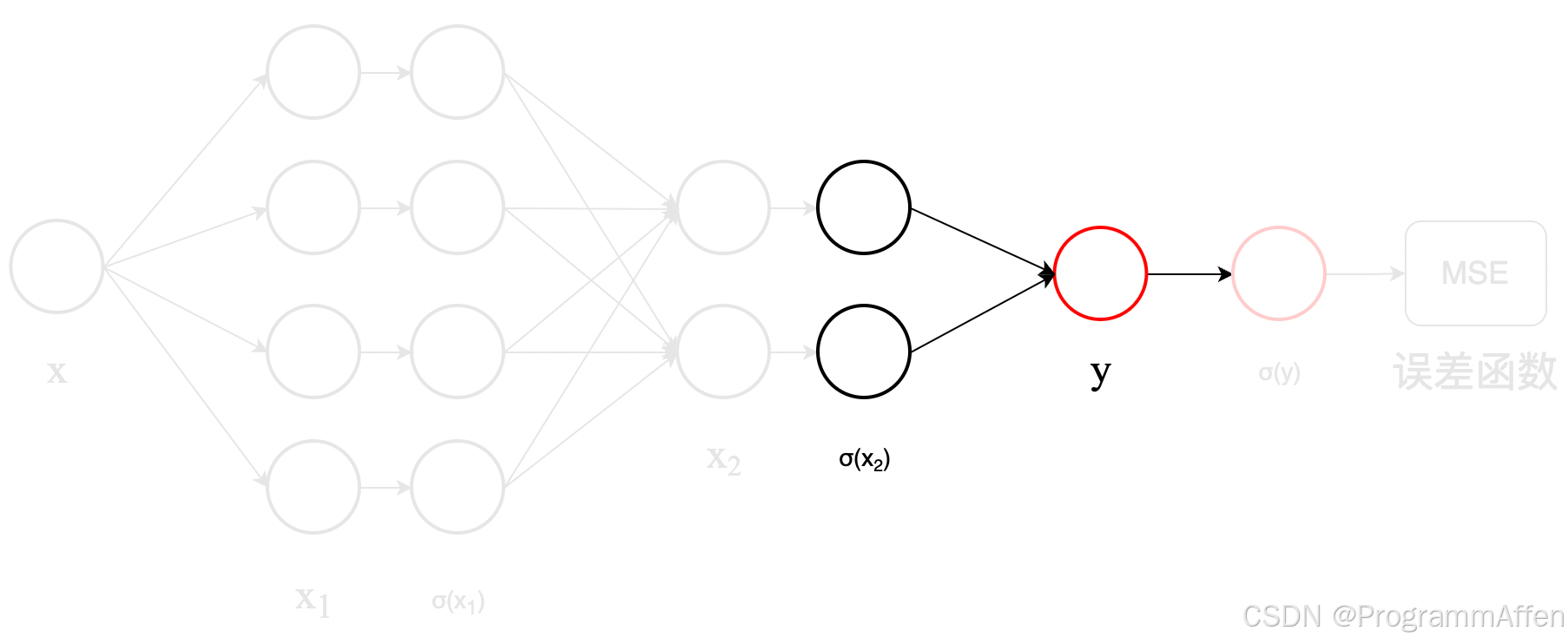
首先来看
σ ( x 2 ) \sigma(\boldsymbol{x_2})
σ
(
x
2
) 是怎么到
y \boldsymbol{y}
y 的:
y
W 3 σ ( x 2 ) + b 3 \boldsymbol{y} = \boldsymbol{W_3}\boldsymbol{\sigma(x_2)} + \boldsymbol{b_3}
y
=
W
3
σ
(
x
2
)
b
3
写成矩阵相乘的形式:
[ y ]
[ w 11 3 w 12 3 ] ⋅ [ σ ( x 11 2 ) σ ( x 21 2 ) ] \begin{bmatrix} y \ \end{bmatrix} = \begin{bmatrix} w_{11}^3 & w_{12}^3 \ \end{bmatrix} \cdot \begin{bmatrix} \sigma(x_{11}^2) \ \sigma(x_{21}^2) \end{bmatrix}
[
y
]
=
[
w
11
3
w
12
3
]
⋅
[
σ
(
x
11
2
)
σ
(
x
21
2
)
]
其中
w 11 3 w_{11}^3
w
11
3
表示
W 3 \boldsymbol{W_3}
W
3
矩阵的1行1列,也就是下标表示在矩阵中的位置,上标表示序号,
σ ( x 2 ) \boldsymbol{\sigma(x_2)}
σ
(
x
2
) 也是一样。
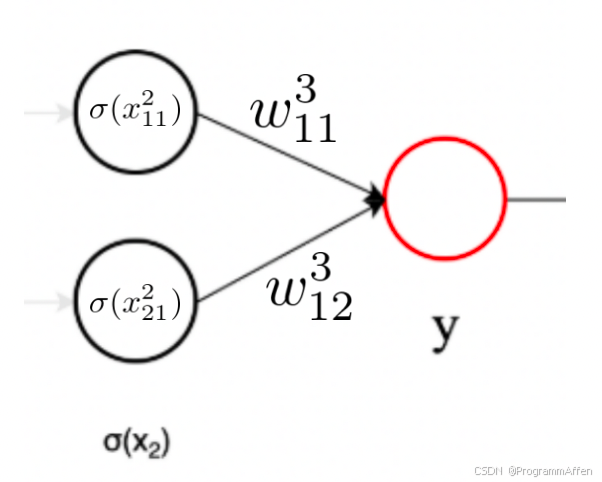
写成算式:
y
w 11 3 ⋅ σ ( x 11 2 ) + w 12 3 ⋅ σ ( x 21 2 ) y = w_{11}^3 \cdot \sigma(x_{11}^2) + w_{12}^3\cdot \sigma(x_{21}^2)
y
=
w
11
3
⋅
σ
(
x
11
2
)
w
12
3
⋅
σ
(
x
21
2
)
那么
y \boldsymbol{y}
y 对
W 3 \boldsymbol{W_3}
W
3
的导数依然是一个偏导数:
d y d W 3
[ ∂ y ∂ w 11 3 ∂ y ∂ w 12 3 ]
[ σ ( x 11 2 ) σ ( x 21 2 ) ] \frac{dy}{d\boldsymbol{W_3}} = \begin{bmatrix} \frac{\partial y}{\partial w_{11}^3} &\frac{\partial y}{\partial w_{12}^3} \end{bmatrix} = \begin{bmatrix} \sigma(x_{11}^2) & \sigma(x_{21}^2) \end{bmatrix}
d
W
3
d
y
=
[
∂
w
11
3
∂
y
∂
w
12
3
∂
y
]
=
[
σ
(
x
11
2
)
σ
(
x
21
2
)
]
那么根据梯度下降算法更新的
W 3 \boldsymbol{W_3}
W
3
就如下式,注意不要忘记前面传导过来的误差:
W 3 ′
[ w 11 3 − α ⋅ d ( M S E ) d σ ( y ) d σ ( y ) d y σ ( x 11 2 ) w 12 3 − α ⋅ d ( M S E ) d σ ( y ) d σ ( y ) d y σ ( x 21 2 ) ] \boldsymbol{W’3} = \begin{bmatrix} w{11}^3 - \alpha \cdot \frac{d(MSE)}{d\sigma(y)}\frac{d\sigma(y)}{dy} \sigma(x_{11}^2) & w_{12}^3 - \alpha \cdot \frac{d(MSE)}{d\sigma(y)} \frac{d\sigma(y)}{dy}\sigma(x_{21}^2) \end{bmatrix}
W
3
′
=
[
w
11
3
−
α
⋅
d
σ
(
y
)
d
(
MSE
)
d
y
d
σ
(
y
)
σ
(
x
11
2
)
w
12
3
−
α
⋅
d
σ
(
y
)
d
(
MSE
)
d
y
d
σ
(
y
)
σ
(
x
21
2
)
]
对
b \boldsymbol{b}
b 的误差的求导也很简单,因为
b 3 \boldsymbol{b_3}
b
3
是个常数矩阵,导数就是1,读者可以自行推导一下。
下一次前向传播用的就是更新后的
W 3 ′ \boldsymbol{W’_3}
W
3
′
和
b 3 ′ \boldsymbol{b’_3}
b
3
′
了。
**4)
y \boldsymbol{y}
y 的误差传导给
σ ( x 2 ) \boldsymbol{\sigma(x_2)}
σ
(
x
2
) 层**
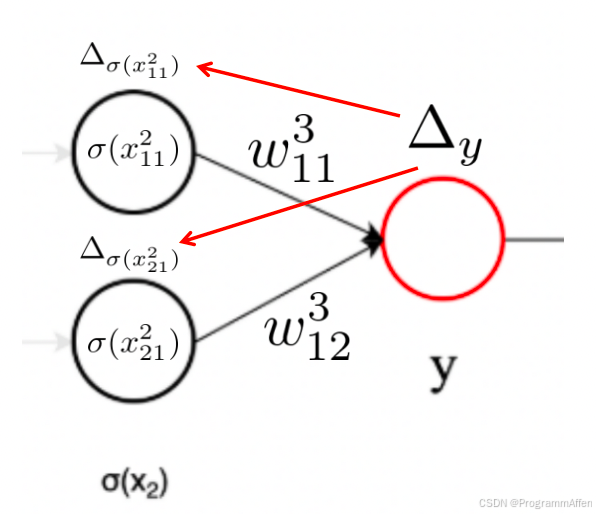
误差还得继续向前面传递,我们把从均方误差函数传导到
y \boldsymbol{y}
y 为止的误差记作
Δ y \Delta_y
Δ
y
,在3)中利用
Δ y \Delta_y
Δ
y
求得了针对
W 3 \boldsymbol{W_3}
W
3
和
b 3 \boldsymbol{b_3}
b
3
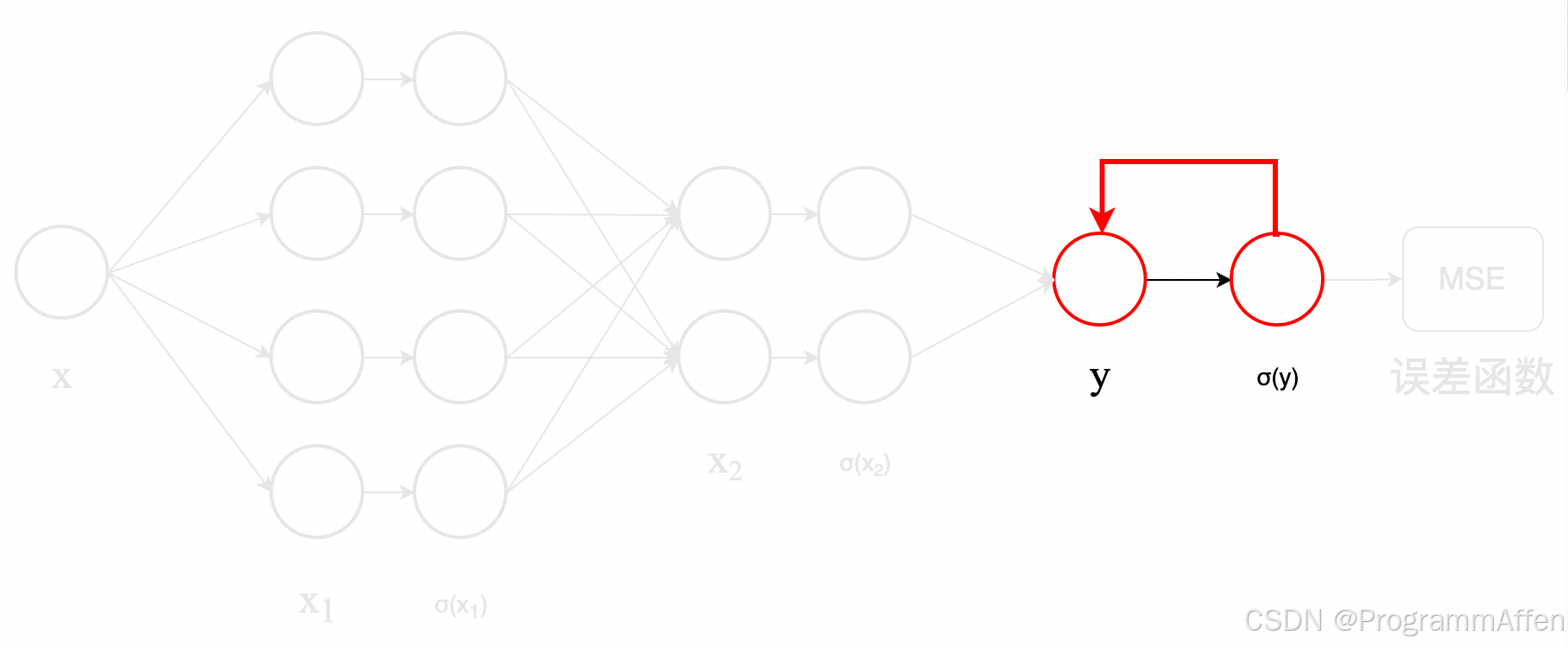
的导数,现在要把
Δ y \Delta_y
Δ
y
传递给
σ ( x 2 ) \boldsymbol{\sigma(x_2)}
σ
(
x
2
) 层,如下图所示:
其实这个过程不难,因为从
σ ( x 2 ) \boldsymbol{\sigma(x_2)}
σ
(
x
2
) 到
y \boldsymbol{y}
y 的过程相乘的矩阵
W 3 \boldsymbol{W_3}
W
3
的维度是
( 1 , 2 ) (1, 2)
(
1
,
2
) ,那么你只需要让
y \boldsymbol{y}
y 的维度的矩阵
W 3 \boldsymbol{W_3}
W
3
相乘变回
σ ( x 2 ) \boldsymbol{\sigma(x_2)}
σ
(
x
2
) 的维度就可以了。
从
σ ( x 2 ) \boldsymbol{\sigma(x_2)}
σ
(
x
2
) 到
y \boldsymbol{y}
y 的维度变化:
( 1 , 2 ) ⋅ ( 2 , 1 ) → ( 1 , 1 ) (1, 2) \cdot (2,1) \rightarrow (1,1)
(
1
,
2
)
⋅
(
2
,
1
)
→
(
1
,
1
)
从
y \boldsymbol{y}
y 返回
σ ( x 2 ) \boldsymbol{\sigma(x_2)}
σ
(
x
2
) 的维度变化:
( 2 , 1 ) ⋅ ( 1 , 1 ) → ( 2 , 1 ) (2, 1) \cdot (1,1) \rightarrow (2,1)
(
2
,
1
)
⋅
(
1
,
1
)
→
(
2
,
1
)
也就是说误差
Δ y \Delta_y
Δ
y
从
y \boldsymbol{y}
y 传播到
σ ( x 2 ) \boldsymbol{\sigma(x_2)}
σ
(
x
2
) :
Δ σ ( x 2 )
W 3 T ⋅ Δ y \boldsymbol{\Delta_{\sigma(x_2)}} = \boldsymbol{W_3^T} \cdot \boldsymbol{\Delta_y}
Δ
σ
(
x
2
)
=
W
3
T
⋅
Δ
y
注意:
这里使用的
W 3 T \boldsymbol{W_3^T}
W
3
T
是没有经过梯度下降更新的
W 3 \boldsymbol{W_3}
W
3
,而不是 KaTeX parse error: Double superscript at position 17: …boldsymbol{W’_3^̲T} 。
这样就完成了误差从
y \boldsymbol{y}
y 返回
σ ( x 2 ) \boldsymbol{\sigma(x_2)}
σ
(
x
2
) 层的传递,接下来的事情就是重复3)和4)直到更新完
W 1 \boldsymbol{W_1}
W
1
。
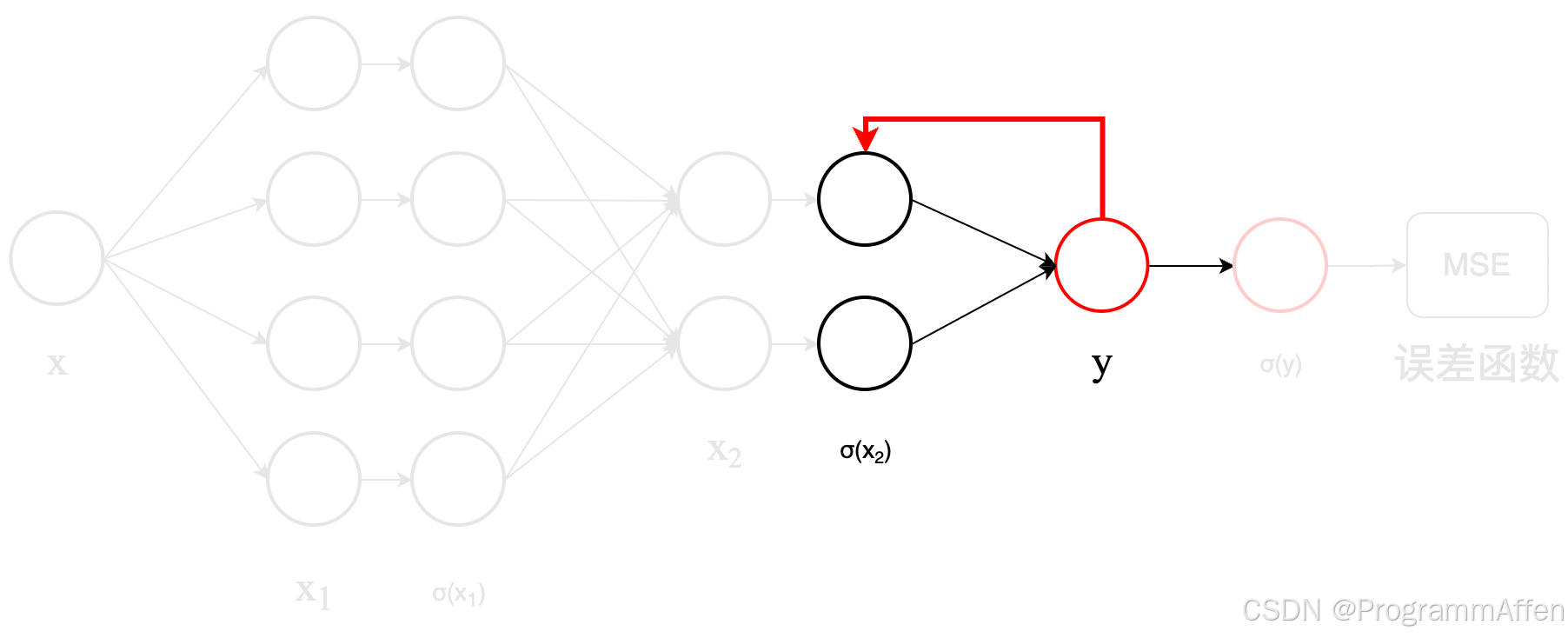
这样一轮前向传播一轮反向传播就是一次训练,被称为一个epoch,训练多轮使得输入与输出的结果相近。
2.4 小结
在学习反向传播的时候,一开始也是比较懵的,最好是用笔写一下矩阵乘法的维度,多比划几次就能弄清楚了;此外最好也是不借助深度学习的框架去写一下正向传播和反向传播的代码,因为有些计算结果需要保留后续给反向传播使用,以及一些边界条件也需要注意。