考研机试常见基本题型c

目录
考研机试常见基本题型(c++)
1、求100以内的素数
sqrt()函数在cmath头文件中。
#include <iostream>
#include <cmath>
using namespace std;
int main() {
int count = 0; // 用于统计素数的个数
// 遍历 100 到 200 之间的每一个数
for (int num = 100; num <= 200; num++) {
bool isPrime = true; // 先假设当前数是素数
// 判断是否为素数,检查从 2 到根号 num 的数
for (int i = 2; i <= sqrt(num); i++) {
if (num % i == 0) {
isPrime = false; // 如果能整除,则不是素数
break;
}
}
if (isPrime) {
count++; // 如果是素数,计数器加 1
cout << num << " "; // 输出素数
}
}
cout << endl << count << endl; // 换行后输出素数的个数
return 0;
}2、判断某点是否在一个三角形内
1、面积法
abs()、sqrt()都是在cmath中
#include <iostream>
#include <vector>
#include <cmath>
// 计算两点间距离
double distance(std::vector<double>& a, std::vector<double>& b) {
return std::sqrt((a[0] - b[0]) * (a[0] - b[0]) + (a[1] - b[1]) * (a[1] - b[1]));
}
// 计算三角形面积
double triangleArea(std::vector<double>& a, std::vector<double>& b, std::vector<double>& c) {
double ab = distance(a, b);
double bc = distance(b, c);
double ca = distance(c, a);
double s = (ab + bc + ca) / 2;
return std::sqrt(s * (s - ab) * (s - bc) * (s - ca));
}
// 判断点是否在三角形内
bool isPointInTriangle(std::vector<double>& p, std::vector<double>& a, std::vector<double>& b, std::vector<double>& c) {
double s = triangleArea(a, b, c);
double s1 = triangleArea(p, a, b);
double s2 = triangleArea(p, b, c);
double s3 = triangleArea(p, c, a);
// 考虑浮点数精度问题,判断差值是否在一个很小的范围内
return std::abs(s - (s1 + s2 + s3)) < 1e-9;
}
int main() {
// 测试代码
std::vector<double> a = {0, 0};
std::vector<double> b = {1, 0};
std::vector<double> c = {0, 1};
std::vector<double> p = {0.2, 0.2};
std::cout << (isPointInTriangle(p, a, b, c)? "在三角形内" : "不在三角形内") << std::endl;
return 0;
}3、鸡兔同笼
#include <iostream>
using namespace std;
// 判断是否能构成有效的鸡兔同笼问题
bool isSameCage(int heads, int feet) {
// 判断脚的数量减去两倍头的数量是否为偶数且大于等于0
if ((feet - 2 * heads) % 2 == 0 && feet - 2 * heads >= 0) {
int y = (feet - 2 * heads) / 2; // 兔子的数量
int x = heads - y; // 鸡的数量
// 判断鸡和兔的数量是否都为非负整数
if (x >= 0 && y >= 0) {
return true;
}
}
return false;
}
int main() {
// 测试用例
cout << (isSameCage(35, 94)? "true" : "false") << endl;
cout << (isSameCage(2, 4)? "true" : "false") << endl;
cout << (isSameCage(4, 2)? "true" : "false") << endl;
cout << (isSameCage(10, 30)? "true" : "false") << endl;
return 0;
}4、英文字母大小写转换
描述:把一个字符串中所有的大写字母转换为小写字母,小写字母转换为大写字母,其他字符保持不变。
#include <iostream>
#include <string>
using namespace std;
int main() {
string s;
cin >> s;
for (char& c : s) {
if (isupper(c)) {
c = tolower(c);
} else if (islower(c)) {
c = toupper(c);
}
}
cout << s << endl;
return 0;
}c语言版本
#include <iostream>
#include <string>
using namespace std;
int main() {
string s;
cin >> s;
for (char& c : s) {
if ('A'<=c && c<='Z') {
c +=32;
}
else if ('a' <= c && c <= 'z') {
c -=32;
}
}
cout << s << endl;
return 0;
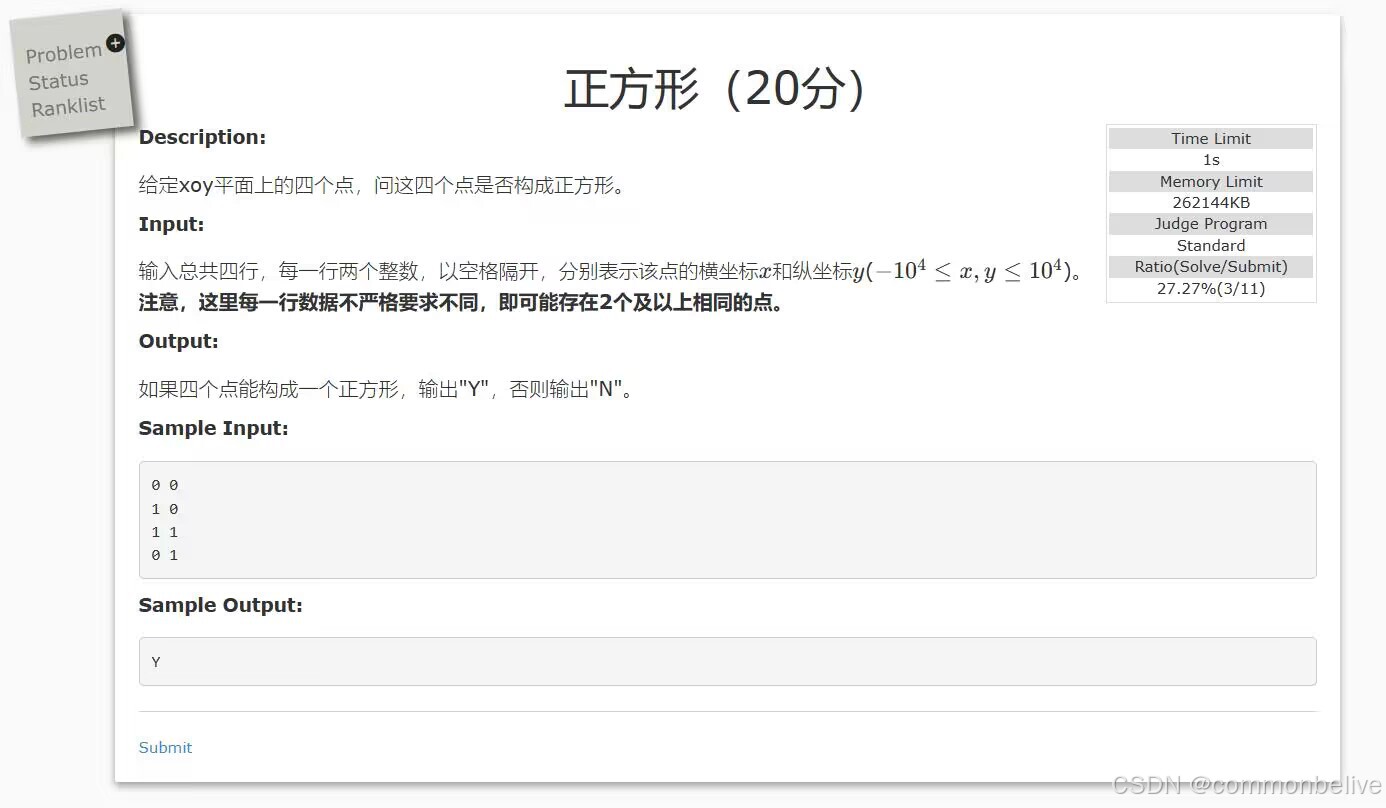
}判断是否为正方形
#include<stdio.h>
#include<iostream>
#include<sstream>
#include<vector>
#include<string>
#include<algorithm>
using namespace std;
//判断是否为正方形:正方形的四条边长度相等,对角线长度相等,且对象线长度为边长的根号2倍
// 难点:四个点并不是按照顺序输入的。
//1、本题只计算 边长的平方,对角线的平方 , 能给计算带来方便
//2、本题还有一个巧的地方:就是四个点中两两之间的线段刚好就是6条
int distanceSquare(int x1, int y1, int x2, int y2)
{
return (y1 - y2) * (y1 - y2) + (x1 - x2) * (x1 - x2);
}
int main()
{
vector<vector<int>> square(4, vector<int>(2, 0));
for (int i = 0; i < 4; i++)
{
for (int j = 0; j < 2; j++)
{
cin >> square[i][j];
}
}
vector<int> distance;
distance.push_back(distanceSquare(square[0][0], square[0][1], square[1][0], square[1][1]));
distance.push_back(distanceSquare(square[1][0], square[1][1], square[2][0], square[2][1]));
distance.push_back(distanceSquare(square[2][0], square[2][1], square[3][0], square[3][1]));
distance.push_back(distanceSquare(square[3][0], square[3][1], square[0][0], square[0][1]));
distance.push_back(distanceSquare(square[0][0], square[0][1], square[2][0], square[2][1]));
distance.push_back(distanceSquare(square[1][0], square[1][1], square[3][0], square[3][1]));
sort(distance.begin(), distance.end());
if (distance[0] == distance[1] && distance[1] == distance[2] && distance[2] == distance[3]
&& distance[4] == distance[5] && distance[5] == 2 * distance[0])
{
cout << "Y";
}
else
{
cout << "N";
}
return 0;
}