论文阅读 Quantum Convolutional neural network

摘要：我们介绍并分析了由卷积神经网络激励的新型量子机学习模型。我们的量子卷积神经网络（QCNN）仅利用O(log(n))的变异参数来实现N量子位的输入大小，从而可以对现实，近期量子设备进行有效的训练和实施。 QCNN架构结合了多尺度的纠缠重新归一化ANSATZ和量子误差校正。我们通过两个例子明确说明了其潜力。首先，QCNN用于准确识别与 1D对称保护拓扑 相关的量子状态。我们从数值上证明，在一小组可溶解点上训练的QCNN可以在整个参数方面重现相图，并提供精确的，分析的QCNN解决方案。作为第二个应用程序，我们利用QCNN来设计针对给定误差模型优化的量子错误校正方案。我们提供了一个通用框架，以同时优化编码和解码程序，并发现所得方案显着超过了可比复杂性的已知量子代码。最后，讨论了QCNN的潜在实验实现和概括。

专业术语

quantum phase recognition（QPR）

quantum error correction（QEC）(用于检测和纠正局部量子错误而不坍缩波函数的机制)

multiscale entanglement  renormalization ansatz（MERA）多尺度纠缠重整化推测 — 用于多体波函数的重要变分推测

背景

基于神经网络的机器学习在许多实际应用中取得了重大进展。在物理学中，一个自然的应用方向是研究量子多体系统，由于多体态的极端复杂性，往往使得理论分析难以处理。这促使了最近一系列利用机器学习来研究量子系统特性的成果，利用物理概念来解释机器学习，或者利用量子计算机来增强传统机器学习任务。在本研究中，受实现量子信息处理器进展的启发，我们通过提出一种受机器学习启发的量子电路模型，将这些方法结合起来，并展示了其在两类重要的量子多体问题上的成功应用。

我们考虑的第一类问题是量子相位识别（QPR），它询问给定的输入量子态 是否属于某一特定的量子物质相。关键在于，与许多基于张量网络描述的现有方案不同，我们假设 是在一个物理系统中制备的，而没有直接访问其经典描述。

第二类问题是量子纠错（QEC）优化，它要求为给定的、先验未知的错误模型（如退相干或实际实验环境中的潜在相关去极化）找到最优的 QEC 码。

尽管使用大规模神经网络的传统机器学习能够成功解决类似的经典问题，如图像识别或改进经典纠错，但庞 大的多体希尔伯特空间 阻碍了在不进行指数量级困难的量子态或过程层析成像的情况下，将这些量子问题有效地转化为经典框架。 量子算法避免了这种开销 ，但近期量子设备的有限尺寸和相干时间阻止了大规模网络的使用；因此 ，首先从理论上理解必须实现的最重要的机器学习机制至关重要 。在这项工作中，我们介绍了一种用于QPR和QEC优化的量子机器学习方法，为其成功提供了理论见解和数值演示，并展示了其在近期实验中实现的可行性。

QCNN的电路实现

卷积神经网络（CNN）为图像识别等分类任务提供了成功的机器学习架构。CNN通常由一系列不同（交错）的图像处理层组成；在每一层中，从上一层生成一个中间的二维像素数组，称为特征图（feature map）（图1a）。卷积层通过对前一特征图中的邻近像素进行线性组合来计算新的像素值：

其中 是一个 的矩阵。池化层通过从几个相邻像素中取最大值来减小特征图的大小，并且通常后面会应用非线性（激活）函数。一旦特征图的大小足够小，最终的输出是通过一个依赖于所有剩余像素的函数计算得出的（即全连接层）。这些权重和全连接函数通过在大型数据集上训练来优化。与此相对，卷积层和池化层的数量以及权重矩阵的大小 w（即超参数）在特定的CNN中是固定的。 CNN的关键特性是卷积和池化层的平移不变性，每层的参数数量是恒定的（与系统大小无关），并且数据大小逐步减少（即层次结构） 。基于这一架构，我们引入了一种量子电路模型，将这些关键特性扩展到量子领域（图1b）。电路的输入是一个未知的量子态 ​。卷积层在有限深度内以平移不变的方式应用单一的准局部单位算符（ ​）。对于池化操作，一部分量子比特会被测量，并且它们的测量结果决定了应用于邻近量子比特的单位旋转（

因此，量子卷积神经网络（QCNN）的非线性来自于自由度的减少。卷积和池化层将一直执行，直到系统大小足够小；然后，应用一个全连接层作为剩余量子比特的单位算符 F。最后，通过测量固定数量的输出量子比特得到电路的结果。与经典情况类似，电路结构（即QCNN的超参数）如卷积层和池化层的数量是固定的，而单位算符本身是通过学习得到的。 用于分类N 量子比特输入态的QCNN因此由 O(log⁡(N) 个参数表征 。这与一般的基于量子电路的分类器相比，提供了双指数量级的降维，从而实现了高效的学习和实现。例如，给定分类训练数据 (∣ψα​⟩,yα​):α=1,…,M}，其中 ∣ψα​⟩ 为输入态，yα=0或 1为对应的二分类输出，可以计算均方误差（MSE）：

电路模型与量子信息理论中两个著名的概念——多尺度纠缠重整化推测（MERA）和量子纠错（QEC）相联系。MERA框架为许多类有趣的多体波函数提供了高效的张量网络表示，包括与临界系统相关的波函数。MERA可以被理解为一个由一系列单位算符和同胚层作用在输入态（例如 ∣00⟩上的量子态。每个同胚层都会在应用单位算符之前引入一组新的量子比特，并将其置于预定的状态（如 ∣0⟩）；单位算符层则简单地对现有量子比特应用准局部单位算符（图1c）。这种指数增长的层次结构能够引入与临界系统相关的长程关联。QCNN电路具有类似的结构，但其运行方向是相反的。因此，对于任何给定的状态∣ψ⟩，如果它具有MERA表示，就总是存在一个QCNN能够识别∣ψ⟩ 并产生确定的测量结果；一个这样的QCNN实际上就是MERA电路的逆。但是，对于其他的输入态，QCNN通常并不会产生确定的测量结果。这些额外的自由度将QCNN与MERA区分开来。具体来说，我们可以将测量视为量子纠错（QEC）中的综合测量，这些测量决定了要应用于剩余量子比特的纠错单位算符 Vj​。因此，一个具有多个池化层的QCNN电路可以视为MERA（用于多体波函数的重要变分推测）和嵌套QEC（用于检测和纠正局部量子错误而不坍缩波函数的机制）的组合。这使得QCNN成为一种强大的架构，用于分类输入量子态或设计新的QEC编码方案。特别是，对于量子相位识别（QPR），QCNN可以提供代表目标相位的量子态 ∣ψ0​⟩ 的MERA实现。同一相位中的其他输入态可以视为在局部错误下的 ∣ψ0​⟩，这些局部错误会通过QCNN的多个层进行纠正。从这个角度来看，QCNN电路可以模拟重整化群（RG）流动，这是一种成功分类多类量子相的理论方法。对于QEC优化，QCNN结构可以同时优化高效的编码和解码方案，并可能具有丰富的纠缠结构。

(a) 文章主要讨论的哈密顿量的相图。相边界点（蓝色和红色菱形）来自无限尺寸密度矩阵重整化群（DMRG）数值模拟，而颜色表示输入大小为 N=45 自旋时，精确 QCNN 电路的输出结果（见方法部分）。

(b) 识别 Z2​×Z2​ 对称保护拓扑（SPT）相的精确 QCNN 电路。蓝色线段表示受控相位门，蓝色三量子比特门为 Toffoli 门，控制量子比特位于 X 基底中，而 橙色双量子比特门用于当 X 测量结果为 -1 时翻转目标量子比特的相位 。全连接层应用受控相位门，然后进行 Xi​ 投影，从而有效地测量 Zi−1​Xi​Zi+1（pauli x改变量子比特的状态，pauli z改变量子比特的相位）​。

(c) 沿着 h1=0.5J方向，N=135 自旋系统的 QCNN 输出结果，深度 d=1,…,4。

(d) 深度为 d=1,…4 的 QCNN 采样复杂度（蓝色）与 SOP（字符串序列）方法检测 SPT/顺磁相变的采样复杂度（红色）对比。 红色曲线对应 SOP 长度分别为 N/2,N/3,N/5,N/6N/2, N/3, N/5, N/6N/2,N/3,N/5,N/6。临界点由无限尺寸 DMRG 确定为 h2/J=0.423（加粗线）。颜色加深表示 QCNN 深度增加或字符串序列长度缩短。在阴影区域，相关长度超过系统大小，有限尺寸效应可能会显著影响结果。插图：绘制了 SOP 方法与 QCNN 方法的采样复杂度比值，作为深度 d 的函数，纵坐标为对数刻度。在数值可及的范围内，该采样复杂度的减少呈指数缩放关系，符合 （拟合趋势线）。

方法——过程

在多体系统中，我们具体考虑一个 Z2×Z2对称保护拓扑（SPT）相 P（该相包含 S=1 Haldane 链）以及一族作用于具有开放边界条件的自旋-1/2 链上的哈密顿量的基态 {∣ψG⟩}：

其中 Xi和 Zi 是作用在第 i 个自旋上的泡利算符，而 Z2×Z2对称性由

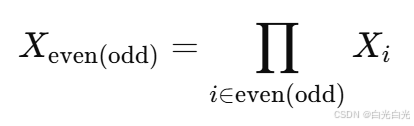
生成。图中给出了相图，其横纵坐标分别为 h1/J 与 h2/J。当 h2=0 时，该哈密顿量可通过 Jordan-Wigner 变换精确求解，证明相 P 是由非局域序参量表征的；而当 h1=h2=0时，各项彼此对易，一个基态即为一维簇态。 我们的目标是确定从相图中抽取的未知基态是否属于 P， 作为示例，我们首先展示了一个精确解析的 QCNN 电路来识别 P（见图b）。该电路中，卷积层使用受控相位门以及以 X 基底为控制的 Toffoli 门；池化层则在相邻某处测量结果为 X=−1 时对剩余量子比特执行相位翻转操作。这个卷积–池化单元重复执行 d 次，其中 d为 QCNN 的深度 。全连接层则对剩余量子比特执行 Zi−1XiZi的测量。图2c展示了在 N=135 自旋系统下、沿 h2=0.5J 方向，不同深度（d=1,…,4）的QCNN输出结果，该结果由矩阵积态模拟获得。随着 ddd 的增加，测量结果在临界点附近的变化变得更加陡峭，且 d=2 的电路输出已经能高精度地重现相图（图）。此外，该QCNN还可用于其他属于同一相的哈密顿量模型，例如 S=1 Haldane 链（详见方法部分）。

采样复杂度

一个量子相位识别（QPR）求解器的性能可以用采样复杂度来量化，即识别其量子相所需输入态拷贝的期望数量。我们证明，精确QCNN电路的采样复杂度明显优于传统方法。原则上，可以通过测量字符串序参量（SOP） 的非零期望值来检测相 P——例如，定义一个字符串序参量为

然而，在实际中，由于临界点附近相关长度发散，SOP 的期望值趋于零；而在此区域量子投影噪声达到最大，因此需要大量实验重复以确认非零期望值。相比之下，QCNN输出在相变附近更为陡峭，因此所需重复次数较少。定量地，对于给定的输入态 ∣ψin⟩和 SOP S，对 S 的投影测量可视为一个（广义）伯努利随机变量，其输出为1的概率为

而输出为 −1 的概率为 1−p因 ）。经过 M次二元测量后，我们估计p。当 p>p0=0.5 时，即可判断 ∣ψin⟩|属于 P。我们定义采样复杂度 Mmin​ 为在使用反正弦方差稳定化变换下，以95%置信水平测试 p>p0 所需的最小 M：

同理，QCNN 的采样复杂度可通过将表达式中的 ⟨ψin∣S∣ψin⟩ 替换为QCNN输出的期望值得到。图2d展示了不同QCNN深度和不同长度SOP下的采样复杂度。从图中可以明显看出，在整个参数区间内，QCNN所需的输入拷贝数远少于SOP方法，尤其在临界附近尤为明显。更重要的是，尽管SOP的采样复杂度与字符串长度无关，QCNN的采样复杂度则随着深度的增加持续改善，并且在我们的模拟中仅受限于有限尺寸效应。特别地，与SOP方法相比，QCNN将采样复杂度降低的因子在数值可及的区域中呈指数随QCNN深度增长（见插图）。这种缩减源于每一深度下反复执行的量子纠错（QEC），而这种效应不可能通过对简单（可能非局域）的观测获得。我们在方法部分证明，QCNN电路实际上测量的是一个多尺度字符串序参量——即一个由指数多个不同SOP乘积之和构成的量，该量在临界边界附近依然保持尖锐。

尺度纠缠重整化推测（MERA）以及量子纠错（QEC）

通过将 QCNN 与多尺度纠缠重整化推测（MERA）以及量子纠错（QEC）联系起来，可以进一步洞察 QCNN 的性能 。具体而言，我们的 QCNN 设计上包含了 1D 簇态（∣ψ0⟩的 MERA 表示——该簇态是当 h1=h2=0时哈密顿量 H 的基态，从而使其成为一个稳定的不动点。当将 ∣ψ0⟩| 输入时，每个卷积-池化单元都在未测量的量子比特中产生相同的 ∣ψ0⟩| 状态且系统规模减小，同时在测量的量子比特上获得确定的结果（X=1）。全连接层则测量 Zi−1XiZi​。（图示部分展示了集群模型 QCNN 卷积-池化单元对具有单量子比特 X 错误的状态的作用，见图 3。）

图 4 则展示了一个随机初始化并训练后的 QCNN 在 N=15 自旋、深度 d=1 下的输出。灰色点显示了（大部分）训练数据点， 这些数据点是 Hamiltonian 可通过 Jordan-Wigner 变换求解的直线上 40 个等距采样点（在 h2=0 且 h1∈[0,2]的情况下） ；蓝色和红色菱形则是从无限尺寸 DMRG 数值模拟中提取的相边界点，而颜色表示 QCNN 输出的期望值。

对于 ∣ψ0⟩| 的 SOP，当输入波函数偏离 ∣ψ0⟩| 时，QCNN 能够纠正这种“错误”。例如，如果发生单个 X 错误，第一层池化操作会识别出错误位置，然后通过受控单位操作对沿电路传播的错误进行修正（见图 3）。 类似地，如果初始状态存在多个且足够分离的错误（可能以相干叠加的方式存在），经过若干次卷积和池化层后，错误密度将明显降低。如果输入状态最终收敛到不动点，QCNN 就能以高保真度将其归类到 SPT 相中 。显然，这一机制类似于基于重整化群（RG）流动的量子相分类方法。

图 5：(a) QCNN 优化量子纠错（QEC）的示意图。逆 QCNN 将一个逻辑量子比特 ∣ψl⟩编码为 9 个物理量子比特，这些量子比特随后受到噪声 N 的影响；QCNN 再对其进行解码以获得逻辑状态 ρ\rhoρ。 我们的目标是最大化 ⟨ψl∣ρ∣ψl⟩ 。 (b) 在一个相关错误模型下，Shor 码（蓝色）与经过学习得到的 QEC 码（橙色）的逻辑错误率对比。输入错误率定义为所有概率 pμ​ 与 pxxp_{xx}pxx​ 的和。Shor 码的表现甚至比不进行任何纠错（即使用恒等操作，灰色线）更差，而经过优化的纠错码能够显著降低错误率。

训练 QCNN 得到一个分类器的说明

在每个深度处使用四个卷积层和一个池化层，之后接一个全连接层（见方法部分）。初始时，所有单位算符均设置为随机值。由于对训练过程进行经典模拟需要消耗大量计算资源，我们将焦点放在一个相对较小的系统上，即 N=15N=15N=15 个自旋，且 QCNN 深度 d=1d=1d=1；总共需要学习 1309 个参数（见方法部分）。我们的训练数据由沿 h2=0h_2=0h2​=0 直线上 40 个等间距采样点构成，在该直线上哈密顿量可以通过 Jordan-Wigner 变换精确求解。利用均方误差函数 (1) 和梯度下降法，我们迭代更新各个单位算符直至收敛（详见方法部分）。所得 QCNN 对于一般 h2h_2h2​ 的分类输出如图 4 所示。值得注意的是，该 QCNN 能够准确重现整个参数区间内的二维相图，尽管模型仅在一组可解样本上进行训练，而这组样本甚至没有穿越下部相边界。

这一实例说明了 QCNN 结构如何通过参数数量呈指数减少来避免对训练数据的过拟合。虽然对于这一特定的量子相位识别（QPR）问题，训练数据集由可解点构成，但更一般地，这样的数据集可以通过传统方法（例如测量字符串序参量 SOP）来获取，以分类那些可以通过数值或实验高效生成的代表性状态 。

优化量子纠错（QEC）

正如前例所示，QCNN 的架构使得实现高效 QEC 成为可能。接下来，我们利用这一特性设计一种全新的 QEC 码，该码针对特定错误模型经过优化。更具体地说，任何 QCNN 电路（及其逆电路）都可以看作是物理输入量子比特与逻辑输出量子比特之间的解码（或编码）量子通道。编码方案在预定状态（例如 ∣0⟩|0\rangle∣0⟩）下引入一组新的量子比特，而解码方案则通过测量实现（见图 5a）。给定一个错误通道 NNN 后，我们的目标是最大化恢复保真度

其中 Mq（以及 分别是由 QCNN 电路生成的编码（解码）方案 是泡利算符的 ±1 本征态。因此，我们的方法同时对编码和解码方案进行优化，同时确保它们在实际系统中能够高效实现。更重要的是，由于 fq可通过实验评估，即使错误通道 N 未知，也可以进行变分优化。

为了说明这一过程的潜力，我们考虑一个由两层 QCNN 构成的系统，其物理量子比特数 N=9且含有 126 个可变参数（见图 5a及方法部分）。这一特定架构包含了嵌套的（经典）重复码和 9 量子比特的 Shor 码；在下面的讨论中，我们将我们的性能与这两者中表现更好的进行比较。我们考虑三种不同的输入错误模型：（1）对所有量子比特施加独立的单量子比特错误，且对 X,Y,错误的概率均为 pμ​；（2）各错误的概率不等，即 px≠py=pz；（3）在独立的单量子比特各向异性错误基础上，还增加了相邻两个量子比特之间的相关错误 XiXi+1，其概率为 pxx​。

在将所有 QCNN 参数初始化为随机值后，我们通过数值优化使 fqf_qfq​ 最大化。结果发现，在情况（1）下，我们的模型产生的逻辑错误率与现有的纠错码相同，但在情况（2）下，根据具体的输入错误概率比例（例如当 px=1.8py时可降低 14%，或当 px=0.4py时可降低 50%——详见方法部分），错误率可降低一个常数因子。更为显著的是，在情况（3）下，经过优化的 QEC 码的表现明显优于已知的纠错码（见图 5b）。具体来说，由于 Shor 码仅能保证纠正任意单量子比特错误，其表现甚至比不进行任何纠错（即恒等操作，灰色曲线）还要差，而经过优化的 QEC 码则大大降低了错误率。这一实例展示了利用 QCNN 获得并优化针对现实中先验未知错误模型的新 QEC 码的强大潜力

实验实现

我们的 QCNN 架构可以在几种最先进的实验平台上高效实现。实现 QCNN 的关键条件包括：高效制备量子多体输入态、在不同尺度上施加两量子比特门以及投影测量。这些能力已经在多种可编程量子模拟器中得到验证，这些模拟器基于被困中性原子、离子或超导量子比特，且量子比特数量 N≥50。例如，我们提出了一种可行协议，用于通过中性 Rydberg 原子在近期内实现我们精确簇态模型的 QCNN 电路，在该方案中，长程偶极相互作用允许在可变几何排列下对远距离量子比特执行高保真纠缠门。量子比特可以被编码在超精细基态中，其中一个态可以与 Rydberg 态耦合，从而利用 Rydberg 屏蔽机制执行高效的纠缠操作；方法部分中给出了图 2b 中每个门的具体实现方案。对于一个深度为 d、输入量子比特数为 N 的 QCNN，其所需的多量子比特操作最多为

个，以及 4d次单量子比特旋转。对于实际中有效耦合强度 Ω∼2π×10−100 MHz 和受 Rydberg 态寿命限制的单量子比特相干时间 τ∼200 μs，大约可以执行 Ωτ∼2π×103−104次多量子比特操作，从而实现一个深度 d=4且 N∼100量子比特的 QCNN 是可行的。需要注意的是，这些估计较为保守，因为我们没有考虑诸如脉冲整形⁽⁴⁶⁾等高级控制技术，或者潜在地并行执行独立的多量子比特操作。

方法——理论

正如本文主文所讨论的，（自旋-1/2）一维簇态属于由 Z2×Z2对称性保护的 SPT（对称性保护拓扑）相，而该相还包含著名的 S = 1 Haldane 链 。因此，一个自然的问题是，该量子卷积神经网络（QCNN）是否可以用于检测 Haldane 相与 S = 1 顺磁相 之间的相变。我们在这里通过数值模拟对此进行了验证。

Haldane 链的 Hamiltonian

我们考虑的 Haldane 相对应的 Hamiltonian 定义在一个包含 N 个自旋-1 粒子 的 一维链 上，并具有开边界条件：

其中，Sj表示第 j个站点上的 S = 1 自旋算符 。

该系统受到 Z2×Z2对称性 的保护，该对称性由对所有自旋绕 X 和 Y 轴进行全局 π 旋转 所生成：

当ω为零或远小于 J 时 ，基态属于 SPT 相；但当 ω/J充分大 时，基态变为顺磁态 。

QCNN 识别 Haldane 相

要将 QCNN 电路应用于 Haldane 相，我们需要先找到一个 局部的等距映射 U ，它能在 Haldane 链和簇态模型之间建立联系。因为两者的对称群表示不同，我们要求：

其中， 是簇态模型的对称性。

这样的映射 U 可参考文献构造，其直观思想是 扩展自旋-1 粒子的局部 Hilbert 空间 ，引入一个自旋单态 ∣s⟩，并将其映射为一对自旋-1/2 粒子：

其中，∣+⟩和 ∣−⟩分别是 Pauli 矩阵 X 的 ±1 本征态 。

最终，Haldane 链的 QCNN 电路由 先应用映射 U ，再施加 主文中的 QCNN 电路 组成。

多尺度字符串序参量

我们分析了 QCNN 在 Heisenberg 图像 中测量的最终算符。虽然 QCNN 在池化层 (Pooling) 中进行非幺正测量 ，但与量子纠错 (QEC) 电路类似，我们可以将所有测量推迟到最后，并用 受控门 代替池化层的测量，使 QCNN 等价于测量一个非局域算符 ：

其中：

• i是最终层测量的量子比特索引
• UCP(l)是深度 lll 的卷积-池化单元对应的幺正算符

Pauli 递归关系

我们可以将 QCNN 幺正算符 UCP 与 Pauli 算符对易，得到如下递归关系：

其中，i~ 表示第 l−1 层的比特索引，包括池化层中被测量的比特（见图 8a）。

由此可得，任意形式的字符串序参量 ZXX…XZ 在深度 lll 处会转换为 深度 l−1处的 16 个 SOP（字符串序参量）之线性组合 。因此，QCNN 并非测量单个 SOP，而是测量由指数多个 SOP 线性组合而成的算符 （见图 8）

其中的系数 C 可以通过 递归关系 计算。

总结

1.QCNN成功检测了S=1 Haldane相的拓扑相变，并通过数值模拟准确定位了临界点

2.QCNN 实际测量的是一个多尺度字符串序参量 (SOP) 之和 ，而非单个 SOP，这一特性使其能在长相关长度情况下依然提供清晰的分类结果。

3.QCNN 在 SPT 相的拓扑分类方面具有潜力 ，并展示了其应用于高自旋系统的能力。

为了获得主文中讨论的 QEC 码，我们考虑一个包含 𝑁=9个物理量子比特的 QCNN，并精确模拟其 2𝑁×2𝑁密度矩阵的电路演化。严格来说，我们的 QCNN 包含三层：

第一层是一个包含三个量子比特的卷积层 𝑈1 ；

第二层是一个 3-to-1 的池化层；

第三层是一个 3-to-1 的全连接层 𝑈2；

在不失一般性的前提下，我们可以将池化层的优化吸收到第一层卷积层中，从而得到一个有效的两层电路。然后，通过使用有限差分方法计算均方误差函数关于每个参数 cμ​ 的梯度，

每个参数按照

进行更新，其中 η是本次迭代的学习率。学习率采用 Bold Driver 技术进行调整：如果误差较上一迭代下降 5%，则 η增加 5%；否则减少 50%。这种梯度下降过程不断重复，直至误差函数变化量达到 10^{-5} 量级

构造 QCNN 电路

为了构造图 2b 中的精确 QCNN 电路，我们遵循主文中讨论的指导原则，设计卷积和池化层时满足以下两个重要性质：

1. 不动点准则 ：如果输入为 L个自旋的簇态 ∣ψ0⟩，则卷积—池化层的输出为 L/3个自旋的簇态 ∣ψ0⟩，且所有测量都确定性地得到 ∣0⟩。
2. 量子纠错（QEC）准则 ：如果输入状态不是 ∣ψ0⟩，而是与 ∣ψ0⟩ 在某一站点上存在一个与全局对称性对易的错误，则输出依然为 L/3 个自旋的簇态，但至少有一个测量结果会得到 ∣1⟩。

这两个性质对于任何用于 RG 流（重整化群流）实现 QPR 的量子电路都是理想的。对于我们具体的 Hamiltonian，当 H=−J∑iZiXi+1Zi+2的未扰动情形下，其基态（1D 簇态）正好构成了一个稳定的码空间，其稳定子为 {ZiXi+1Zi+2}。因此，QCNN 的卷积和池化层的剩余自由度被设计为在存在单量子比特 X 错误时能检测并纠正错误（即至少一次测量输出为 ∣1⟩），从而防止错误传播到下一层。

QCNN 用于通用 QPR 问题

我们对 QCNN 的解释（基于 MERA 和 QEC 的观点）激励了将其应用于更一般的量子相位识别问题。对于任何量子相 P，只要其 RG 不动点波函数 ∣ψ0(P)⟩具有等距或 G-等距形式的张量网络表示（见图 10a），就可以系统地构造出对应的 QCNN 电路。这类相包括所有一维 SPT 相和二维字符串网相。在这种情况下，可以显式构造出 ∣ψ0(P)⟩的交换父 Hamiltonian 以及一个使 ∣ψ0(P)⟩ 成为不动点波函数的 MERA 结构（如图 10a 所示）。图 10b 给出了不动点性质的图示证明。此外，任何将输入状态从 ∣ψ0(P)⟩ 扰动出的“局部错误”都可以通过测量父 Hamiltonian 中的部分项来识别，类似于基于稳定子测量的 QEC。于是，针对相 P 的 QCNN 电路就由 ∣ψ0(P)⟩的 MERA 表示和嵌套的 QEC 方案组成，其中当输入状态的错误密度低于 QEC 阈值时，它将“流向” RG 不动点。这样一个 QCNN 可以通过我们的学习过程进行优化。虽然我们的通用学习协议从完全随机的单位算符开始（与经典情形相同），但这种初始化对于梯度下降来说可能不是最有效的。受到深度学习预训练技术的启发，更好的初始参数化应当基于 ∣ψ0(P)⟩| 的 MERA 表示和某种嵌套 QEC 方案，通过学习过程优化 QEC 方案，从而将其阈值扩展到目标相边界（见图 10c）。

图10

实验资源分析

为了估计在 Rydberg 原子实现下簇态模型 QCNN 电路的门深度，我们对图 2b 中每个门进行了分析。通过将池化层的测量推迟到电路末端，所需的多量子比特门包括

量子信息论

图 11： 对于各向异性去极化错误模型，我们绘制了 Shor 码与 QCNN 码逻辑错误率的比值。我们固定总输入错误率 ptot=px+py+pz=0.001 且令 py=pz，同时改变 px/ptot的比例。

通用的三量子比特幺正操作 U1 和 U2​ 分别用 63 个 Gell-Mann 系数进行参数化。正如主文中所讨论的，我们考虑三种不同的错误模型：

1. 对所有量子比特施加独立的单量子比特错误，其错误概率对于 X、Y 和 Z 均为 pμ；
2. 对所有量子比特施加独立的单量子比特错误，但具有各向异性，即 px≠py=pz​；
3. 对所有量子比特施加独立的各向异性单量子比特错误，并额外施加概率为 pxx的相邻量子比特 XiXi+1 的相关错误。

更具体地，前两种错误模型通过对九个物理量子比特的每一个施加一个（通常是各向异性的）去极化量子通道来实现：

对于各向异性情况，我们在不同的错误模型下训练了 QCNN，这些模型具有相同的总错误概率 px+py+pz=0.001，但相对比例不同；图 11 将 Shor 码与 QCNN 码逻辑错误率的比值作为各向异性函数绘制出来。对于强各向异性模型，QCNN 的性能优于 Shor 码；而对于近各向同性的模型，Shor 码是最优的，QCNN 也只能达到相同的逻辑错误率。

对于相关错误模型，我们还额外施加了如下量子通道：

作用于相邻的量子比特对，即 i∈{1,2,4,5,7,8}。这种几何局部相关性是出于实验考虑而引入的。在这种情况下，我们在特定错误模型下训练 QCNN 电路，参数选取为 px=5.8×10−3，py=pz=2×10−3，pxx=2×10−4，并评估在不同物理错误模型下（保持相同的相对比例，但每个量子比特的总错误 px+py+pz+pxx​ 不同）逻辑错误率

展望

上述考虑表明，QCNN 为一种有前景的量子机器学习范式。未来可以考虑若干有趣的推广和研究方向。首先，尽管我们只给出了用于识别一维相的 QCNN 电路结构，但将该模型推广到更高维度是很直接的，在更高维中，可以支持具有内在拓扑序（例如 toric 码）的相⁽⁴⁷,⁴⁸⁾。这种研究可能有助于识别对于诸如量子自旋液体⁽⁴⁹⁾或任何子链条⁽⁵⁰⁾等尚不十分清楚的相而言具有低采样复杂度的非局域序参量。为了识别更为奇异的相，我们还可以放宽平移不变性约束，使得系统大小为 NNN 时参数数量达到 O(N)O(N)O(N)，或者利用辅助量子比特来按照传统 CNN 架构实现并行特征映射。进一步的扩展可以结合针对 QEC 码空间容错操作的优化。最后，虽然在我们的学习演示中使用了有限差分方案来计算梯度，但 QCNN 与其经典对应物在结构上的相似性也激励了采用其他梯度估计方法的可能性。

结论

• SOP 方法可以检测 SPT 相，但计算复杂度高（需要较多样本）。
• QCNN（量子卷积神经网络）方法可以更高效地检测相变，且采样复杂度随 QCNN 深度指数级下降。
• QCNN 方法和字符串序参量方法在物理原理上不同，但 QCNN 方法可以有效模拟 SOP，并且更具计算优势

附录

1.什么是字符串序参量（SOP）？

在传统的 局域序参量 （如磁化强度 ⟨Xi⟩）无法有效区分某些拓扑相（如 Haldane 相）时， 字符串序参量（SOP） 提供了一种方法来识别这些相。

字符串序参量的定义通常涉及多个远离的站点之间的 长程关联 ，通常具有如下形式：

其中：

• Zi,Xk,Zj是泡利矩阵（Pauli operators）。
• 指数项 eiπ∑k=ijXk表示一个相位因子。
• 这意味着我们要计算两个远离站点 i,j 的 Z 分量的关联 ，同时考虑它们之间的 X 作用 。

这个非局域的字符串序参量可以用来检测 对称保护拓扑（SPT）相 ，例如 Haldane 相。

在本文的背景下， SOP 方法 是另一种检测 SPT 相的方式，它与 QCNN 方法进行了对比。文章表明，在检测拓扑相变时，SOP 方法的采样复杂度（即所需的样本数）远高于 QCNN 方法，因此 QCNN 方法更高效。

2.什么是h和j？

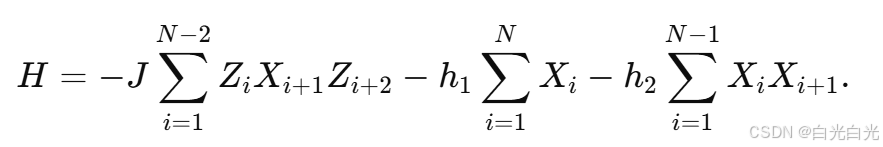
• J 是相互作用强度（Interaction Strength）

  • J 控制的是三体相互作用项 ：ZiXi+1Zi+2。
  • 该项可以用来稳定某些拓扑相（如 SPT 相）。
  • 在 h1=h2=0 时，系统的基态是 一维簇态（1D cluster state） ，它是典型的 SPT 相。

• h1和 h2是横向磁场（Transverse Fields）

  • h1 代表单体的横向场项 Xi ，即每个自旋都受到一个外部磁场的作用。
  • h2​ 代表相邻自旋之间的 Xi​Xi+1​ 相互作用 ，即 Ising 型的耦合项。

三体作用项 ：

是指哈密顿量中涉及三个粒子同时参与相互作用的项，如 −ZiXi+1Zi+2-Z_i X_{i+1} Z_{i+2}−Zi​Xi+1​Zi+2​。这种项可以反映系统更复杂的局部交互，常用于描述拓扑相、量子纠错机制或经过某些有效理论推导后的模型。

3.什么是幺正测量？

在量子力学中， 测量 是获取量子系统信息的过程，而 幺正性 （Unitarity）描述了系统在封闭演化中的特性。以下是两者的详细分析：

基本概念

• 幺正测量（Unitary Measurement）

  严格来说， 标准的量子测量本身是非幺正的 。但“幺正测量”这一术语可能出现在以下两种特殊情境中：

  • 间接测量 ：通过引入辅助系统（如环境或测量装置），将测量过程嵌入到一个更大的幺正演化中。例如，在量子电路中，通过添加量子比特和受控操作实现测量，整体系统的演化是幺正的，但被测系统的状态坍缩依然是非幺正的。
  • 广义测量（POVM） ：使用正算子值测度（Positive Operator-Valued Measure）描述测量，虽然测量算符本身非幺正，但可以通过扩展系统（如引入环境）实现幺正演化。

• 非幺正测量（Non-unitary Measurement）

  指直接导致量子态坍缩的传统测量过程。测量算符（如投影算符）不满足幺正性，且过程不可逆。例如，测量量子比特的基态（如 ∣0⟩ 或 ∣1⟩）会破坏叠加态。