【AI知识】内积、点积、逐元素乘法、矩阵乘法等概念介绍

内积、点积、逐元素乘法、矩阵乘法等等概念傻傻弄不清？T T 记录一下：

1.内积：

内积（Inner Product），也称为点积（Dot Product）或数量积，是指两个向量之间的运算，计算规则是： 两个向量的对应元素相乘后求和，结果是一个标量（一个数值） ，它要求两个向量的长度必须相同，可以用来计算相似度（如余弦相似度）、注意力机制等。

如果再详细一点介绍：

1）内积的数学意义：

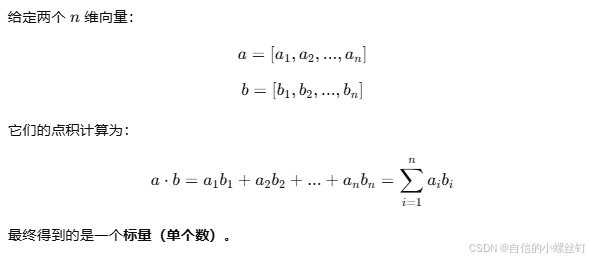
2）内积的几何意义：

cosθ 表示向量方向的相似程度，如果 cosθ 接近 1，说明两个向量方向相近（相似）；如果接近 0，说明它们几乎无关。

2.逐元素乘法

逐元素乘法（Element-wise Multiplication），也称为哈达玛积（Hadamard Product），是指两个相同维度的矩阵或向量中每个对应位置的元素相乘。结果是一个与输入矩阵或向量维度相同的新矩阵或向量。

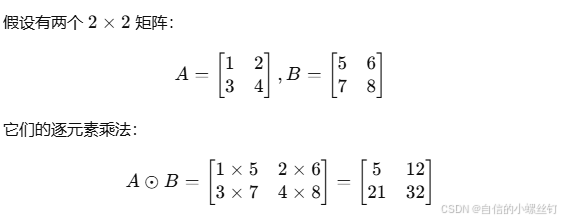
3.矩阵乘法

矩阵乘法（Matrix Multiplication）是指两个矩阵之间的运算，结果是一个新矩阵，计算规则是： 矩阵 𝐴的行向量与矩阵 𝐵 的列向量进行点积，得到新矩阵 ，要求左侧矩阵的列数必须等于右侧矩阵的行数。应用如深度学习的全连接层（Linear Layer），自注意力机制中的Q*K^T 计算等。