2022年SCI1区TOP信念空间和广义对立学习自适应差分进化算法ACDEF,深度解析性能实测

2022年SCI1区TOP:信念空间和广义对立学习自适应差分进化算法ACDE/F,深度解析+性能实测

1.摘要
差分进化算法(DE)在解决复杂优化问题时常面临过早收敛和局部优化的挑战。为了解决这些问题,本文提出了一种自适应差分进化算法(ACDE/F),该算法结合了信念空间策略、广义对立学习策略和参数自适应策略。ACDE/F通过引入文化算法的思想和不同的变异策略到信念空间中,平衡了全局探索能力和局部优化能力。广义对立学习策略提高局部优化过程的收敛速度并增加种群的多样性。此外,ACDE/F提出了参数自适应调整策略,合理调整变异因子和交叉因子,以避免陷入局部最优。
2.改进策略
信念空间策略
ACDE/F算法结合了文化算法和差分进化算法,分为两个空间:种群空间和信念空间。种群空间由DE算法生成的初始种群构成,而信念空间则分为两类。
情境知识
情境知识由当前找到的最优个体
E E
E 组成,
E E
E 代表了其他个体的学习对象。为了初始化
E E
E ,在种群初始化过程中需要评估适应度值,以便选择最优个体。变异算子:
x i , j ′
E i + F ∗ ( x i , r 1 − x i , r 2 ) x_{i,j}^{\prime}=E_{i}+F*(x_{i,r1}-x_{i,r2})
x
i
,
j
′
=
E
i
F
∗
(
x
i
,
r
1
−
x
i
,
r
2
)
规范知识
规范知识包括决策变量的区间,根据进化迭代后的更优解,决策变量的区间会发生变化,从而提高算法的收敛性。
X i , j ′
{ X i , r 3 + F ⋅ ∣ X i , r 1 − X i , r 2 ∣ if X i , r 3 < l i X i , r 3 − F ⋅ ∣ X i , r 1 − X i , r 2 ∣ if X i , r 3
u i X i , r 3 + F ⋅ ∣ X i , r 1 − X i , r 2 ∣ d m i i otherwise X’{i,j} = \begin{cases} X{i,r3} + F \cdot |X_{i,r1} - X_{i,r2}| & \text{if } X_{i,r3} < l_i \ X_{i,r3} - F \cdot |X_{i,r1} - X_{i,r2}| & \text{if } X_{i,r3} > u_i \ X_{i,r3} + \frac{F \cdot |X_{i,r1} - X_{i,r2}|}{dmi_i} & \text{otherwise} \end{cases}
X
i
,
j
′
=
⎩
⎨
⎧
X
i
,
r
3
F
⋅
∣
X
i
,
r
1
−
X
i
,
r
2
∣
X
i
,
r
3
−
F
⋅
∣
X
i
,
r
1
−
X
i
,
r
2
∣
X
i
,
r
3
d
m
i
i
F
⋅
∣
X
i
,
r
1
−
X
i
,
r
2
∣
if
X
i
,
r
3
<
l
i
if
X
i
,
r
3
u
i
otherwise
规范知识更新时,主要变化的是上下界:
l i
{ X i , m i n i if X i , m i n i < l i ∨ f ( X m i n i ) < L i l i otherwise l_i = \begin{cases} X_{i,min_i} & \text{if } X_{i,min_i} < l_i , \vee , f(X_{min_i}) < L_i \ l_i & \text{otherwise} \end{cases}\
l
i
=
{
X
i
,
mi
n
i
l
i
if
X
i
,
mi
n
i
<
l
i
∨
f
(
X
mi
n
i
)
<
L
i
otherwise
u i
{ X i , m a x i if X i , m a x i
u i ∨ f ( X m a x i )
U i u i otherwise u_i = \begin{cases} X_{i,max_i} & \text{if } X_{i,max_i} > u_i , \vee , f(X_{max_i}) > U_i \ u_i & \text{otherwise} \end{cases}
u
i
=
{
X
i
,
ma
x
i
u
i
if
X
i
,
ma
x
i
u
i
∨
f
(
X
ma
x
i
)
U
i
otherwise
自适应参数策略
F i
{ F i − 1 if f i t i , n e x t ≤ f i t i F 0 + k ⋅ τ if f i t i , n e x t
f i t i and τ < 0.5 1 − k ⋅ τ else F_i = \begin{cases} F_{i-1} & \text{if } fit_{i,next} \leq fit_{i} \ F_0 + k \cdot \tau & \text{if } fit_{i,next} > fit_{i} \text{ and } \tau < 0.5 \ 1 - k \cdot \tau & \text{else} \end{cases}
F
i
=
⎩
⎨
⎧
F
i
−
1
F
0
k
⋅
τ
1
−
k
⋅
τ
if
f
i
t
i
,
n
e
x
t
≤
f
i
t
i
if
f
i
t
i
,
n
e
x
t
f
i
t
i
and
τ
<
0.5
else
C R i
{ C R i − 1 if f i t i , n e x t ≤ f i t i C R 0 + k ⋅ τ if f i t i , n e x t
f i t i and τ < 0.5 1 − k ⋅ τ else CR_i = \begin{cases} CR_{i-1} & \text{if } fit_{i,next} \leq fit_{i} \ CR_0 + k \cdot \tau & \text{if } fit_{i,next} > fit_{i} \text{ and } \tau < 0.5 \ 1 - k \cdot \tau & \text{else} \end{cases}
C
R
i
=
⎩
⎨
⎧
C
R
i
−
1
C
R
0
k
⋅
τ
1
−
k
⋅
τ
if
f
i
t
i
,
n
e
x
t
≤
f
i
t
i
if
f
i
t
i
,
n
e
x
t
f
i
t
i
and
τ
<
0.5
else
流程图
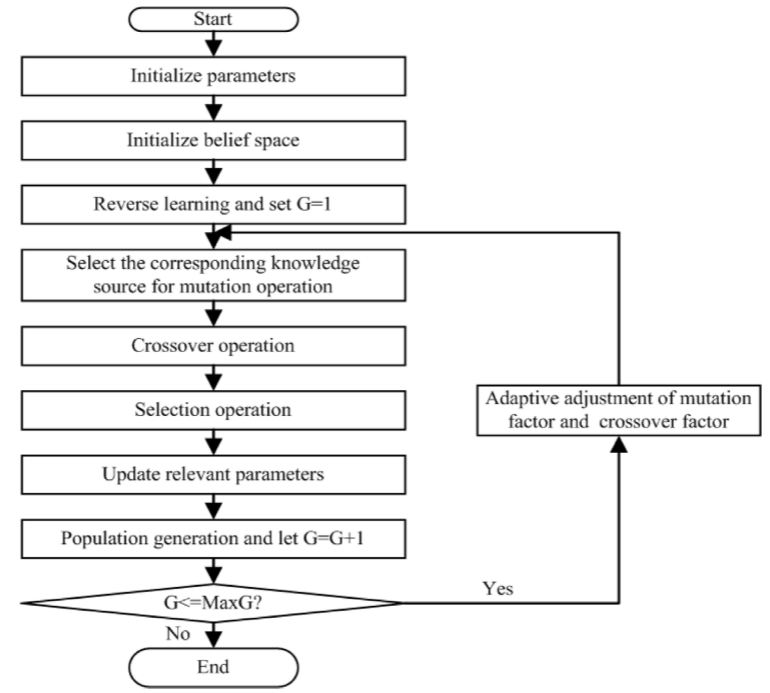
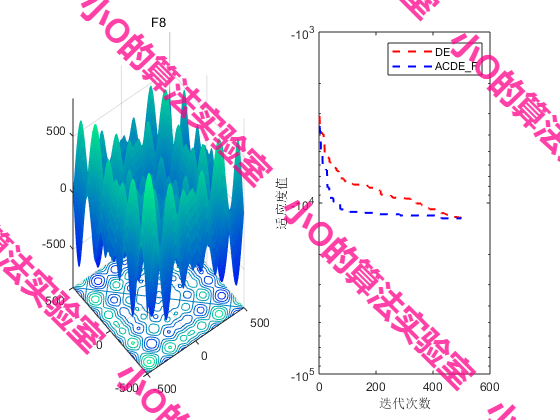
3.结果展示
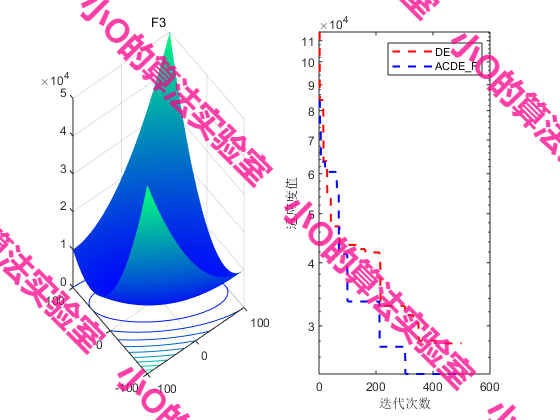
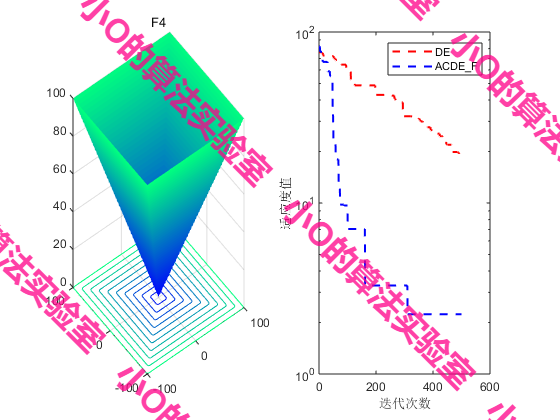
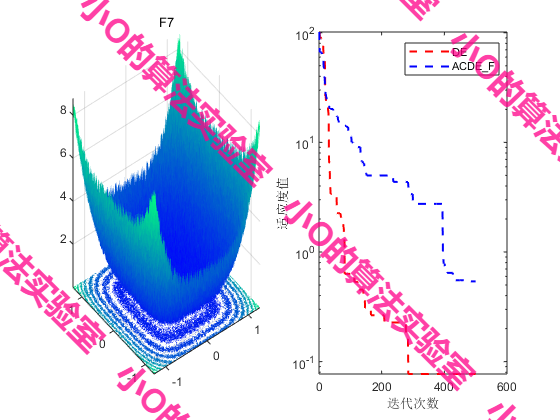
4.参考文献
[1] Deng W, Ni H, Liu Y, et al. An adaptive differential evolution algorithm based on belief space and generalized opposition-based learning for resource allocation[J]. Applied Soft Computing, 2022, 127: 109419.