2025.3.2机器学习笔记PINN文献阅读

2025-03-13 约 5014 字预计阅读 11 分钟

https://bing.ee123.net/img/rand?artid=146149242

2025.3.2机器学习笔记：PINN文献阅读

一、文献阅读

题目信息

题目： 1-D coupled surface flow and transport equations revisited via the physics-informed neural network approach
期刊： Journal of Hydrology
作者： Jie Niu, Wei Xu, Han Qiu, Shan Li, Feifei Dong
发表时间： 2023
文章链接：

摘要

本周读了一篇PINN在水文应用上的论文，虽然与本人目前的研究方向有所不同，但是里面的研究方法还是值得借鉴。圣维南方程（SVE）和平流-扩散方程（ADE）常用于解决地表水溶质输运问题。但求解SVE - ADE耦合方程存在很多挑战。传统数值方法存在不连续性、数值误差、计算成本高等问题，且对噪声数据适应性差。在水文学领域，PINN已广泛应用于水文领域，但目前缺乏将其应用于求解SVE-ADE耦合方程的研究。本论文目的是评估PINN在不同条件下求解SVE、ADE及其耦合方程的性能和解决如何构建PINN模型、优化模型参数和结构，以及PINN是否适用于含噪声数据的反问题求解等问题。论文中作者构建了PINN模型，在不同初始和边界条件下求解相关方程，对比PINN结果与解析或数值解以评估其准确性和效率。实验结果表明，PINN能在处理少量数据、无网格离散化等方面优于传统数值方法，且适用于含噪声数据的反问题求解。

Abstract

This week, I reviewed a paper on the use of Physics-Informed Neural Networks (PINNs) in hydrology, which, though slightly off my current research path, offers useful methods worth considering. The Saint-Venant Equations (SVE) and Advection-Diffusion Equation (ADE) are standard tools for modeling solute transport in surface water. However, solving the coupled SVE-ADE system is challenging due to issues like discontinuities, numerical errors, high computational costs, and poor handling of noisy data in traditional methods. While PINNs are widely used in hydrology, their application to the coupled SVE-ADE equations remains underexplored. This paper assesses PINNs’ performance in solving SVE, ADE, and their coupling under various conditions, focusing on model construction, parameter optimization, and suitability for noisy data inverse problems. The authors built a PINN model, tested it with different initial and boundary conditions, and compared results with analytical or numerical solutions to evaluate accuracy and efficiency. Results show that PINNs outperform traditional methods in handling limited data and mesh-free approaches, and they are effective for inverse problems with noisy data.

创新点

作者运用PINN方法求解耦合的SVE - ADE方程，能在单个模型中同时模拟流场和浓度场，节省时间并减少误差。且PINN无需时间步迭代，利用散点配点，更灵活且能降低计算成本，还能处理复杂几何和边界条件，在解决含噪声反问题上表现还算可以。

网络架构

ADE的数学表达式为:

∂ C ∂ t

D ∂ 2 C ∂ x 2 − v ∂ C ∂ x − k C \frac{\partial C}{\partial t} = D \frac{\partial^2 C}{\partial x^2} - v \frac{\partial C}{\partial x} - k C

∂

−

∂

−

C 其中：C为溶质浓度； t为时间；

x x

x :为空间维度；

D D

D 为扩散系数；

v v

v 为流速；

k k

k 为一阶衰减率。

此外，论文描述了 SVE-ADE 的联合形式来拟合方程基于质量平衡，考虑了时间变化的流量，表达如下：

∂ ( A c C ) ∂ t

− ∂ ( Q C ) ∂ x \frac{\partial (A_c C)}{\partial t} = -\frac{\partial (Q C)}{\partial x}

∂

(

)

−

∂

(

)

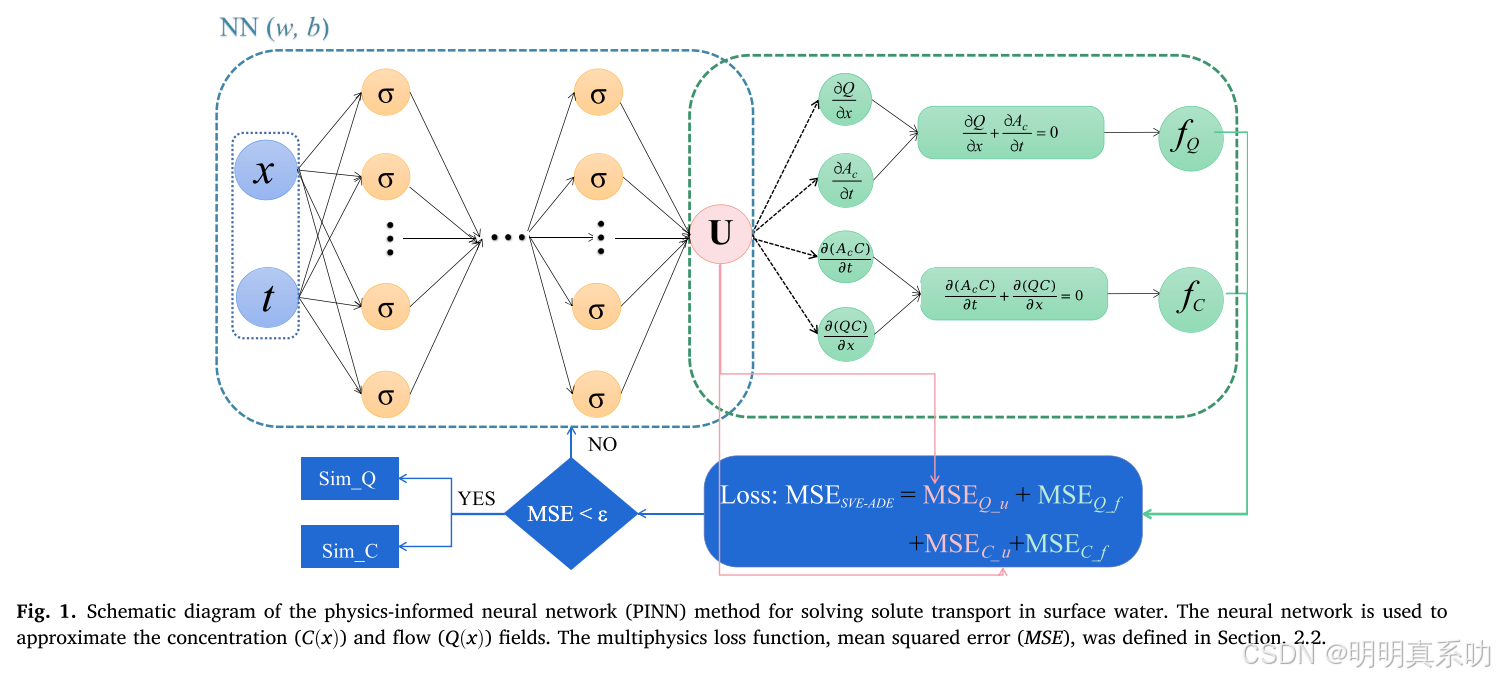
图1展示了论文的PINN架构，如下图所示：

输入层 ：接受空间变量 x 和时间变量 t，表示为 (x,t)。

神经网络 ：一个多层全连接前馈神经网络（NN），参数为 (w,b)

输出层 ：神经网络输出逼近解 U，包括流量 Q(x,t) 和浓度 C(x,t)。

物理约束的残差如下：

SVE残差为

d

∂ Q ∂ x + ∂ A c ∂ t d=\frac{\partial Q}{\partial x}+\frac{\partial A_{c}}{\partial t}

∂

ADE残差为

g

∂ C ∂ t + v ∂ C ∂ x − D ∂ 2 C ∂ x 2 g=\frac{\partial C}{\partial t}+v \frac{\partial C}{\partial x}-D \frac{\partial^{2} C}{\partial x^{2}}

∂

−

∂

SVE-ADE残差为

h

{ ∂ Q ∂ x + ∂ A c ∂ x ∂ ( A c C ) ∂ t + ∂ ( Q C ) ∂ x h=\left{\begin{array}{l}\frac{\partial Q}{\partial x}+\frac{\partial A_{c}}{\partial x} \ \frac{\partial\left(A_{c} C\right)}{\partial t}+\frac{\partial(Q C)}{\partial x}\end{array}\right.

{

∂

(

)

∂

(

)

所以其损失函数为：

M S E Q , u + M S E Q , f + M S E C , u + M S E C , f M S E_{Q, u}+M S E_{Q, f}+M S E_{C, u}+M S E_{C, f}

其中：

M S E Q , u M S E_{Q, u}
MS
E
Q
,
u

，是流量Q关于初始条件和边界条件
M S E Q , u
1 N u ∑ i
1 N u [ Q ( x i , t i ; w , b ) − Q i ∗ ] 2 M S E_{Q, u}=\frac{1}{N_u} \sum_{i=1}^{N_u}\left[Q\left(x_i, t_i ; w, b\right)-Q_i^*\right]^2
MS
E
Q
,
u

=
N
u

1

∑
i
=
1
N
u

[
Q
(
x
i

,
t
i

;
w
,
b
)
−
Q
i
∗

]
2
N u N_u
N
u

个初始/边界条件点；
Q i ∗ Q_i^*
Q
i
∗

为真实值；
M S E Q , f M S E_{Q, f}
MS
E
Q
,
f

是流量Q关于 SVE 方程残差的均方误差。
MSE Q , f
1 N f ∑ j
1 N f [ f Q ( x j , t j ; w , b ) ] 2 \text{MSE}{Q,f} = \frac{1}{N_f} \sum{j=1}^{N_f} \left[ f_Q(x_j, t_j; w, b) \right]^2
MSE
Q
,
f

=
N
f

1

∑
j
=
1
N
f

[
f
Q

(
x
j

,
t
j

;
w
,
b
)
]
2
N f N_f
N
f

为配置点；f是残差，通过自动微分计算物理方程的残差。
同理
M S E C , u M S E_{C, u}
MS
E
C
,
u

与
M S E C , f M S E_{C, f}
MS
E
C
,
f

分别表示浓度C关于 ADE方程残差的均方误差，这里就不再赘述了。

最后设置一个阈值ϵ。若MSE>ϵ，继续回到神经网络中进行对Q和C数值模拟；若MSE<ϵ，输出结果。

实验

本文围绕物理信息神经网络求解ADE、SVE及其耦合方程SVE - ADE展开研究，具体实验结果与数据分析结果如下：

ADE
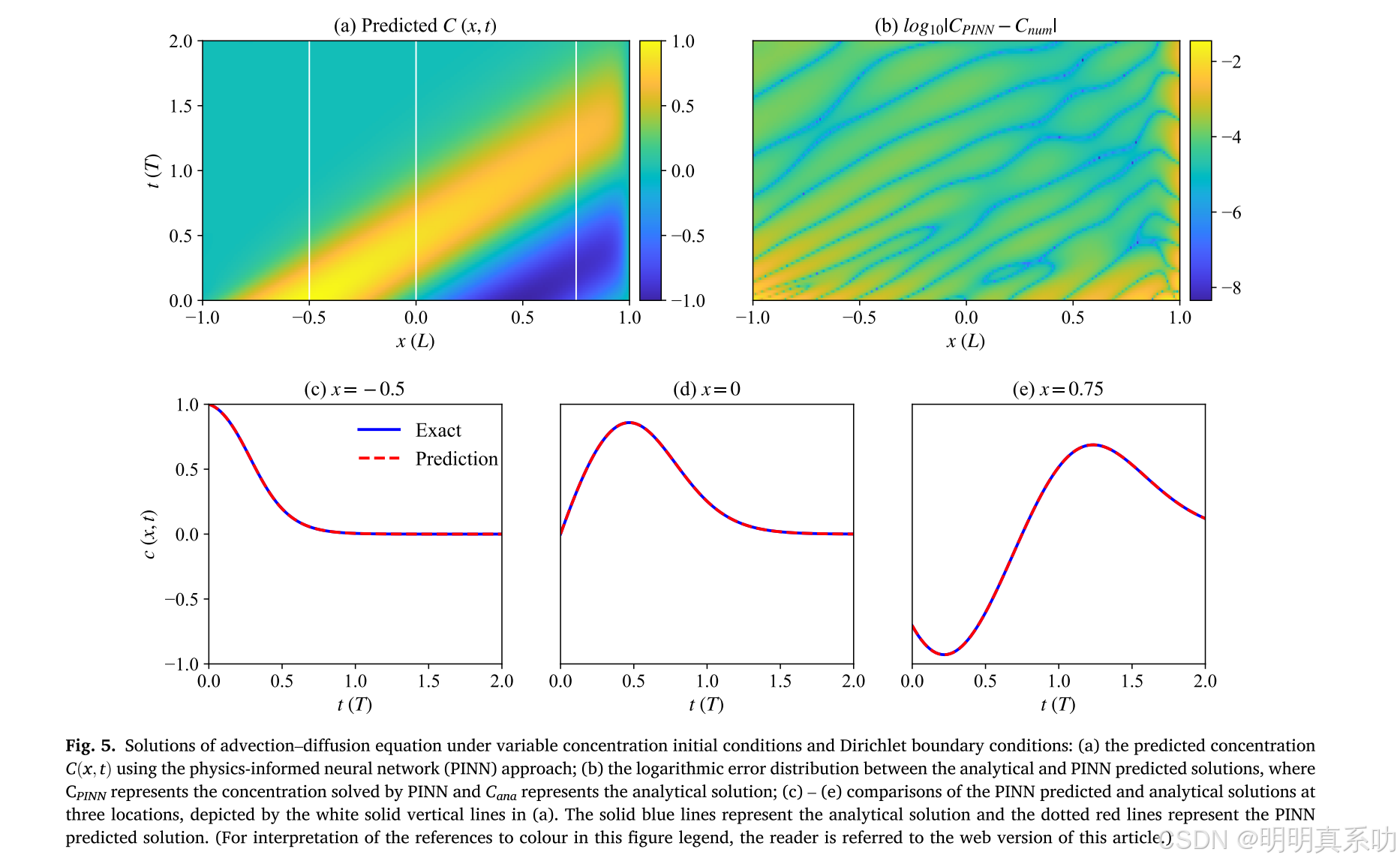
在不同初始与边界条件下的求解精度下，PINN 模型在四种不同初始和边界条件下求解 ADE 均表现良好。 4个不同场景下，如瞬时释放、持续释放等让PINN 预测解与解析解高度吻合，相对 L2 误差分别为 3.6×10 - 3、1.7×10 - 4、9.1×10 - 3 和 1.67×10 - 3。通过调整损失函数中对应惩罚项的权重，PINN 方法能显著降低初始或边界条件下的解误差。
求解SVE及SVE - ADE
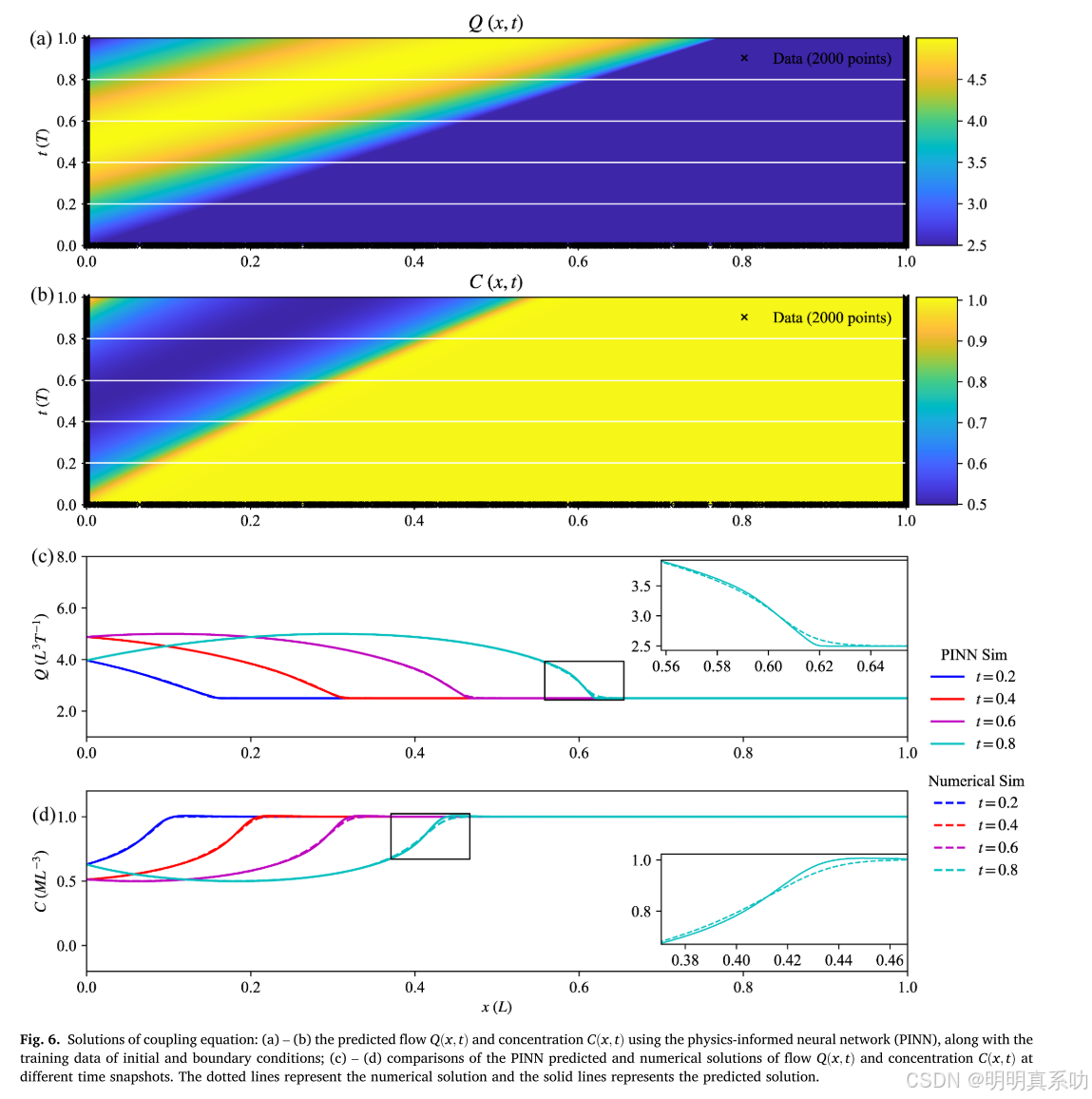
SVE求解结果如下图所示：
PINN 方法求解 SVE 的相对 L2 误差为 7.3×10 -3 ，能够模拟流场。SVE - ADE耦合方程求解结果中，PINN 方法能准确捕捉冲击波行为，而数值解因数值色散在最大流量和浓度附近出现扁平化。流量 Q和浓度C的相对 L2 误差分别为 1.00×10 -3 和 1.36×10 -3 ，进一步证实了 PINN方法的有效性。与传统迭代耦合算法相比，PINN 方法无需时间步迭代，能同时输出流场和浓度场结果，并在训练阶段不断更新网络参数以优化输出，节省时间并减少误差。
PINN求解ADE参数
噪声水平的影响如下图所示：
误差随初始和边界条件点数量的增加而减小，随噪声水平的增加而增大。流速 v 的误差受噪声和 N u 的影响小于一阶衰减率 k 和扩散系数 D。在 1%噪声和 N u = 2000 的条件下，v 和 D 的误差分别为 0.003%和 0.105%，为不同 Nu 值下的最小误差。
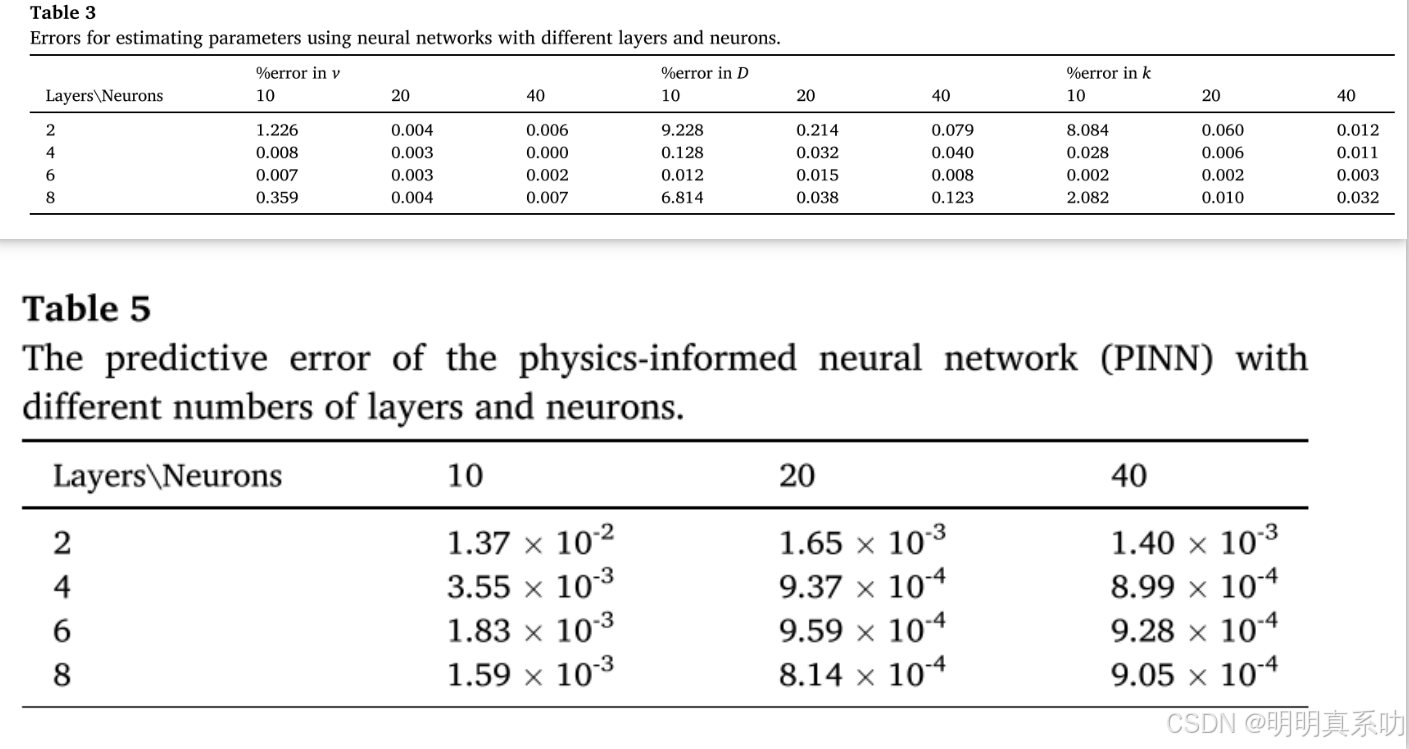
模型结构的影响如下，6 层全连接的 PINN 模型在估计 v、k 和 D 方面表现最佳，2 层 10 个神经元的模型表现最差。8 层 20 个神经元的模型在估计 v、k 和 D 时也表现出色，误差分别为 0.004%、0.038%和 0.010%。
PINN参数设置
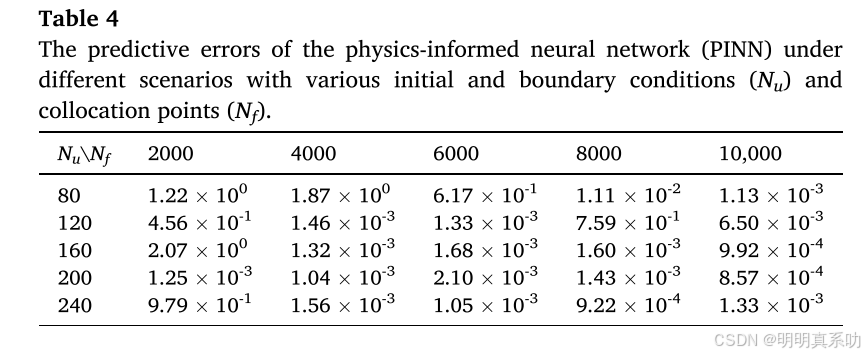
在样本数量的中，在相似的初始和边界条件下，误差随配置点数量的增加而逐渐减小；在相同的配置点条件下，误差随 N u 的增加而减小。PINN 模型在 N u = 200 和 N f = 10000 时误差最小，且当 N u 为 200 时，2000 和 8000 个配置点的误差差异较小，表明 PINN 模型能用较少的 N f 准确模拟结果。
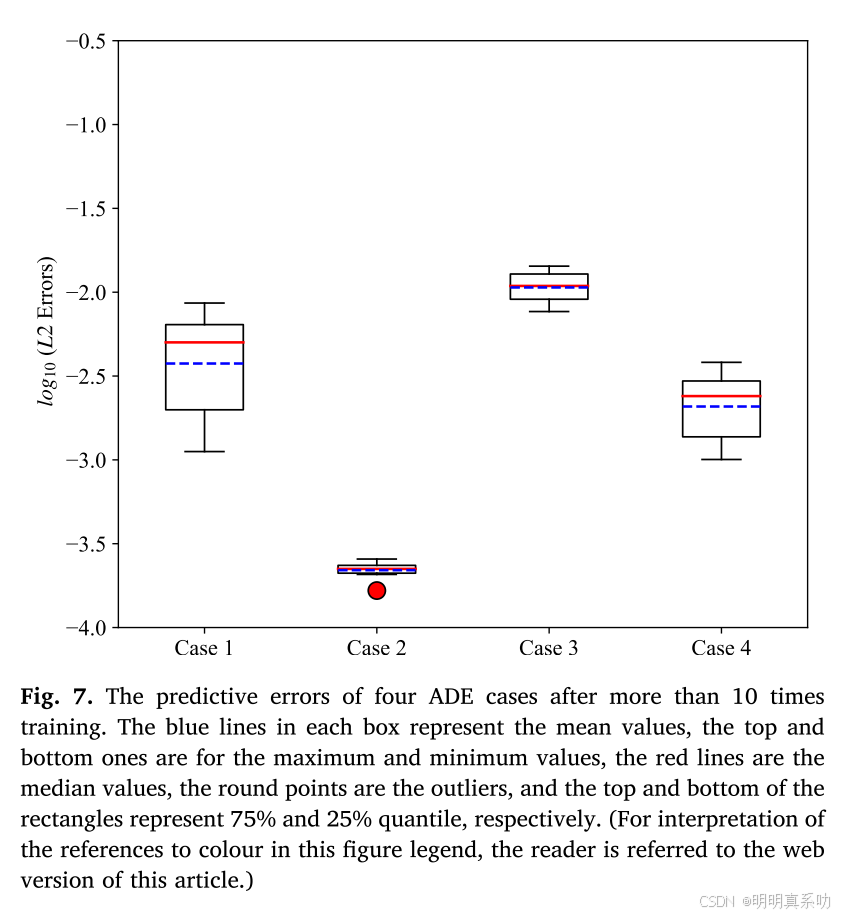
经过 10 次以上不同初始化训练后，四个 ADE 实验结果的平均误差均小于 1.09×10 -2 。每个实验结果的相对 L2 误差浮动范围较小，说明随机种子的设置对模型结果影响不大。优化算法采用 Adam 优化器迭代一定次数确保梯度下降方向正确，再切换到 L - BFGS - B 优化器加速优化直至收敛的两步优化策略。
代码如下：

# 导入必要的库
import torch  # 导入 PyTorch，用于构建神经网络和自动微分
import torch.nn as nn  # 导入 PyTorch 的神经网络模块
import numpy as np  # 导入 NumPy，用于数值计算和数据处理
import matplotlib.pyplot as plt  # 导入 Matplotlib，用于绘图
from scipy.special import erfc  # 导入 SciPy 的误差函数，用于解析解计算

# 设置随机种子，确保结果可重复
torch.manual_seed(1234)  # 设置 PyTorch 随机种子为 1234
np.random.seed(1234)  # 设置 NumPy 随机种子为 1234

# 定义 PINN 模型类，继承自 nn.Module
class PINN(nn.Module):
    def __init__(self, num_hidden_layers=4, num_neurons=20):
        super(PINN, self).__init__()  # 调用父类的构造函数
        # 定义网络结构：输入层 (x, t)，多个隐藏层，输出层 (C)
        self.layers = nn.ModuleList()  # 创建一个模块列表，用于存储网络层
        # 输入层：2 个输入 (x, t)
        self.layers.append(nn.Linear(2, num_neurons))  # 第一个线性层，输入维度 2，输出维度 num_neurons
        # 隐藏层
        for _ in range(num_hidden_layers - 1):
            self.layers.append(nn.Linear(num_neurons, num_neurons))  # 中间隐藏层
        # 输出层：输出 1 个变量 (C)
        self.layers.append(nn.Linear(num_neurons, 1))  # 最后一层，输出 C
        self.tanh = nn.Tanh()  # 定义激活函数为 tanh

    def forward(self, x, t):
        # 前向传播：输入 (x, t)，输出 C
        inputs = torch.cat([x, t], dim=1)  # 将 x 和 t 拼接为一个输入张量，维度为 [batch_size, 2]
        h = inputs  # 初始化隐藏层输入
        # 通过每一层进行前向传播
        for layer in self.layers[:-1]:
            h = self.tanh(layer(h))  # 线性变换后应用 tanh 激活函数
        C = self.layers[-1](h)  # 最后一层不加激活函数，直接输出 C
        return C

    def compute_derivatives(self, x, t):
        # 计算导数：使用自动微分计算 C 关于 x 和 t 的偏导数
        x = x.requires_grad_(True)  # 确保 x 需要计算梯度
        t = t.requires_grad_(True)  # 确保 t 需要计算梯度
        C = self.forward(x, t)  # 前向传播，计算 C

        # 计算 C 的导数
        C_x = torch.autograd.grad(C, x, grad_outputs=torch.ones_like(C), create_graph=True)[0]  # C 对 x 的一阶导数
        C_xx = torch.autograd.grad(C_x, x, grad_outputs=torch.ones_like(C_x), create_graph=True)[0]  # C 对 x 的二阶导数
        C_t = torch.autograd.grad(C, t, grad_outputs=torch.ones_like(C), create_graph=True)[0]  # C 对 t 的一阶导数

        return C, C_x, C_xx, C_t

# 定义解析解函数（Case 1：瞬时释放）
def analytical_solution_case1(x, t, mp=5000, v=1.0, D=0.01):
    # 计算 Case 1 的解析解：瞬时释放的浓度分布
    # 公式：C(x, t) = (mp / (2 * sqrt(pi * D * t))) * exp(-((x - v * t)^2) / (4 * D * t))
    t = np.maximum(t, 1e-6)  # 避免 t = 0 导致除零，使用 1e-6 作为最小值
    C = (mp / (2 * np.sqrt(np.pi * D * t))) * np.exp(-((x - v * t) ** 2) / (4 * D * t))
    return C


def generate_data():
    # Case 1：瞬时释放
    x_domain = [0, 1]  # 空间域：x ∈ [0, 1]
    t_domain = [0, 1]  # 时间域：t ∈ [0, 1]
    v = 1.0  # 流速，单位 L T^-1
    D = 0.01  # 扩散系数，单位 L^2 T^-1
    mp = 5000  # 瞬时释放质量，单位 M

    # 采样点数量
    N_u = 200  # 初始和边界条件点数量
    N_f = 5000  # 内部配点数量

    # 初始条件点 (t = 0)
    x_ic = np.random.uniform(x_domain[0], x_domain[1], N_u)  # 在 x 域 [0, 1] 内均匀随机采样 N_u 个点
    t_ic = np.zeros_like(x_ic)  # t = 0，所有初始条件点的 t 值设为 0
    C_ic = np.zeros_like(x_ic)  # 初始条件：C(x, t=0) = 0，生成 N_u 个零值

    # 边界条件点
    # 左边界 (x = 0)
    t_bc_left = np.random.uniform(t_domain[0], t_domain[1], N_u)  # 在 t 域 [0, 1] 内均匀随机采样 N_u 个点
    x_bc_left = np.zeros_like(t_bc_left)  # x = 0，所有左边界点的 x 值设为 0
    C_bc_left = np.zeros_like(t_bc_left)  # 边界条件：C(x=0, t) = 0，生成 N_u 个零值

    # 右边界 (x = 1)
    t_bc_right = np.random.uniform(t_domain[0], t_domain[1], N_u)  # 在 t 域 [0, 1] 内均匀随机采样 N_u 个点
    x_bc_right = np.ones_like(t_bc_right)  # x = 1，所有右边界点的 x 值设为 1
    C_bc_right = np.zeros_like(t_bc_right)  # 边界条件：C(x=1, t) = 0，生成 N_u 个零值

    # 内部配点
    x_f = np.random.uniform(x_domain[0], x_domain[1], N_f)  # 在 x 域 [0, 1] 内均匀随机采样 N_f 个点
    t_f = np.random.uniform(t_domain[0], t_domain[1], N_f)  # 在 t 域 [0, 1] 内均匀随机采样 N_f 个点

    # 转换为 PyTorch 张量
    x_ic = torch.tensor(x_ic, dtype=torch.float32).reshape(-1, 1)  # 将 x_ic 转换为张量，形状 [N_u, 1]
    t_ic = torch.tensor(t_ic, dtype=torch.float32).reshape(-1, 1)  # 将 t_ic 转换为张量，形状 [N_u, 1]
    C_ic = torch.tensor(C_ic, dtype=torch.float32).reshape(-1, 1)  # 将 C_ic 转换为张量，形状 [N_u, 1]

    x_bc_left = torch.tensor(x_bc_left, dtype=torch.float32).reshape(-1, 1)  # 将 x_bc_left 转换为张量，形状 [N_u, 1]
    t_bc_left = torch.tensor(t_bc_left, dtype=torch.float32).reshape(-1, 1)  # 将 t_bc_left 转换为张量，形状 [N_u, 1]
    C_bc_left = torch.tensor(C_bc_left, dtype=torch.float32).reshape(-1, 1)  # 将 C_bc_left 转换为张量，形状 [N_u, 1]

    x_bc_right = torch.tensor(x_bc_right, dtype=torch.float32).reshape(-1, 1)  # 将 x_bc_right 转换为张量，形状 [N_u, 1]
    t_bc_right = torch.tensor(t_bc_right, dtype=torch.float32).reshape(-1, 1)  # 将 t_bc_right 转换为张量，形状 [N_u, 1]
    C_bc_right = torch.tensor(C_bc_right, dtype=torch.float32).reshape(-1, 1)  # 将 C_bc_right 转换为张量，形状 [N_u, 1]

    x_f = torch.tensor(x_f, dtype=torch.float32).reshape(-1, 1)  # 将 x_f 转换为张量，形状 [N_f, 1]
    t_f = torch.tensor(t_f, dtype=torch.float32).reshape(-1, 1)  # 将 t_f 转换为张量，形状 [N_f, 1]

    return (x_ic, t_ic, C_ic, x_bc_left, t_bc_left, C_bc_left, x_bc_right, t_bc_right, C_bc_right, x_f, t_f), (v, D, mp)

# 训练 PINN 模型
def train_pinn(model, data, params, epochs=10000):
    # 解包数据和参数
    x_ic, t_ic, C_ic, x_bc_left, t_bc_left, C_bc_left, x_bc_right, t_bc_right, C_bc_right, x_f, t_f = data
    v, D, mp = params  # 解包流速 v、扩散系数 D 和瞬时释放质量 mp

    # 定义优化器
    optimizer = torch.optim.Adam(model.parameters(), lr=0.001)  # 使用 Adam 优化器，学习率为 0.001

    # 训练循环
    for epoch in range(epochs):
        optimizer.zero_grad()  # 清空梯度

        # 计算初始条件损失 (MSE_C,u for IC)
        C_ic_pred = model(x_ic, t_ic)  # 预测初始条件下的 C
        mse_C_ic = torch.mean((C_ic_pred - C_ic) ** 2)  # 计算初始条件均方误差

        # 计算左边界条件损失 (MSE_C,u for BC)
        C_bc_left_pred = model(x_bc_left, t_bc_left)  # 预测左边界条件下的 C
        mse_C_bc_left = torch.mean((C_bc_left_pred - C_bc_left) ** 2)  # 计算左边界均方误差

        # 计算右边界条件损失 (MSE_C,u for BC)
        C_bc_right_pred = model(x_bc_right, t_bc_right)  # 预测右边界条件下的 C
        mse_C_bc_right = torch.mean((C_bc_right_pred - C_bc_right) ** 2)  # 计算右边界均方误差

        # 计算内部配点的物理损失 (MSE_C,f for ADE)
        C_f, C_x_f, C_xx_f, C_t_f = model.compute_derivatives(x_f, t_f)  # 计算内部配点导数
        # ADE 方程：∂C/∂t = D * ∂²C/∂x² - v * ∂C/∂x (k = 0)
        f_C = C_t_f - D * C_xx_f + v * C_x_f  # 计算 ADE 残差
        mse_C_f = torch.mean(f_C ** 2)  # 计算 ADE 残差均方误差

        # 总损失
        loss = mse_C_ic + mse_C_bc_left + mse_C_bc_right + mse_C_f  # 总损失：MSE_C,u + MSE_C,f

        # 反向传播和优化
        loss.backward()  # 反向传播，计算梯度
        optimizer.step()  # 更新模型参数

        # 每 1000 次迭代打印损失
        if (epoch + 1) % 1000 == 0:
            print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.6f}')

# 可视化结果
def visualize_results(model, v=1.0, D=0.01, mp=5000):
    # 生成测试点
    x_test = np.linspace(0, 1, 100)  # 在 x ∈ [0, 1] 内生成 100 个均匀点
    t_test = np.linspace(0, 1, 100)  # 在 t ∈ [0, 1] 内生成 100 个均匀点
    X, T = np.meshgrid(x_test, t_test)  # 创建网格点，形状 [100, 100]
    x_flat = torch.tensor(X.flatten(), dtype=torch.float32).reshape(-1, 1)  # 展平 x，形状 [10000, 1]
    t_flat = torch.tensor(T.flatten(), dtype=torch.float32).reshape(-1, 1)  # 展平 t，形状 [10000, 1]

    # 预测浓度 C
    C_pred = model(x_flat, t_flat)  # 使用模型预测 C
    C_pred = C_pred.detach().numpy().reshape(X.shape)  # 转换为 NumPy 数组并重塑为 [100, 100]

    # 计算解析解
    C_analytical = analytical_solution_case1(X, T, mp, v, D)  # 计算解析解

    # 绘制对比图
    plt.figure(figsize=(12, 5))
    plt.subplot(1, 2, 1)
    plt.contourf(X, T, C_pred, levels=50, cmap='jet')  # 绘制 PINN 预测结果的等高线图
    plt.colorbar(label='C (PINN)')  # 添加颜色条，标注为 PINN 预测的 C
    plt.xlabel('x')  # x 轴标签
    plt.ylabel('t')  # t 轴标签
    plt.title('PINN Prediction (Case 1)')  # 标题：PINN 预测结果
    plt.subplot(1, 2, 2)
    plt.contourf(X, T, C_analytical, levels=50, cmap='jet')  # 绘制解析解的等高线图
    plt.colorbar(label='C (Analytical)')  # 添加颜色条，标注为解析解的 C
    plt.xlabel('x')  # x 轴标签
    plt.ylabel('t')  # t 轴标签
    plt.title('Analytical Solution (Case 1)')  
    plt.tight_layout()  # 调整布局，防止重叠
    plt.show()  # 显示图像

# 主函数：运行代码
if __name__ == "__main__":
    # 初始化模型
    model = PINN(num_hidden_layers=4, num_neurons=20)  # 创建 PINN 模型，4 个隐藏层，每层 20 个神经元

    # Case 1：瞬时释放
    print("Training Case 1: Instantaneous Release")
    data, params = generate_data()  # 生成 Case 1 数据
    train_pinn(model, data, params, epochs=10000)  # 训练模型
    visualize_results(model, v=params[0], D=params[1], mp=params[2])  # 可视化结果

结论

本文采用PINN方法求解一维ADE、SVE及其耦合方程。结果表明，PINN能有效结合物理定律，从有限数据中学习PDE解。其精度与初始和边界条件数量、配点数量、网络层数和神经元数量正相关，且噪声数据的影响不大，增加初始和边界条件数量可提高含噪声反问题的模拟精度。

不足以及展望

作者认为当前工作聚焦于规则边界几何的一维问题，对于复杂几何形状和边界条件、非线性和非均质性等方面的处理能力有限。作者希望未来可探索PINN解决二维或三维多物理问题的能力，尤其是处理更复杂几何形状的情况。