AI 界的包青天：GaussianNB 智断分类难题

前言

在机器学习的江湖中，分类算法纷繁复杂，各具特色。有的深不可测，犹如隐世高人的内功心法，让人望而却步；有的则像街头小贩，简单直接却也能精准解决问题。江湖中高手云集，其中有一位侠客，宛如包青天，正气凛然，以公正无私和高效迅捷著称，擅长快速解决分类难题。此侠客正是 Gaussian Naïve Bayes（高斯朴素贝叶斯，简称 GaussianNB）。凭借朴素的假设与强大的数学支撑，GaussianNB 在分类任务中所向披靡，犹如包大人断案，干净利落，一击即中。

在浩瀚的机器学习宇宙中，算法犹如各路江湖门派，各有专长。GaussianNB 如一柄锋利的宝剑，凭借其内功心法——正态分布的数学计算，再加上“条件独立”的轻功步法，能在复杂的数据中迅速找到关键线索，快速解决问题。它并不依赖复杂的套路和冗长的技巧，而是通过简洁高效的数学智慧，把复杂的数据任务轻松化解。这就像江湖中那些看似平凡，却藏有惊人绝技的侠客，往往能一招制敌，令众高手叹服。

应用 GaussianNB 时，首先计算各类别的先验概率，然后利用训练数据中每个特征的均值和方差，推算出其正态分布。最终，依据贝叶斯定理进行推断，得出分类结果。整个过程简洁明快，犹如一场武学比试，每一步都充满精妙，彰显数学和算法的威力。当面对复杂的数据时，GaussianNB 就像一位身怀绝技的侠客，能轻松破解所有疑难，迅速而准确地做出决策。

今天，我们将揭开这位“包青天”的神秘面纱，看看它如何用概率与数学的武功，智断分类难题。GaussianNB 以其简单高效的算法设计，在处理各种分类任务时表现出色。它不需要复杂的操作和深奥的技巧，只需通过精准的计算，就能在数据的江湖中纵横捭阖，快速、高效地解决问题。掌握这个算法，能帮助我们轻松面对分类问题，快速做出决策。

简介

GaussianNB就像是江湖中的一位“武林高手”，以精准、迅速著称。它属于贝叶斯分类器家族，运用的是高斯分布（正态分布）的“绝世武功”。想象一下，每个特征就像江湖中的一个小门派，而GaussianNB的“招式”则假设这些小门派的力量在每个大派（类别）下都遵循着正态分布的规律。它通过这些规律，结合贝叶斯定理，快速判定数据的“身份”，从而完成分类任务。

作为sklearn库中的一员，GaussianNB是一名训练有素的“侦探”。它能通过训练数据，推断出数据所属的标签，这就像包青天通过一堆线索快速破案，不需要复杂的过程，只凭简单的推理就能得出真相。尤其在数据特征独立且符合高斯分布的情况下，它的“武功”得到最大发挥，分类效率极高，处理速度也相当快。

简单说，GaussianNB就像是你的“武林秘籍”，帮助你在分类问题中轻松取胜。不论数据的复杂程度如何，它都能精准地为你找到最可能的分类结果，凭借它的“内力”，让分类任务不再难解。

示例代码

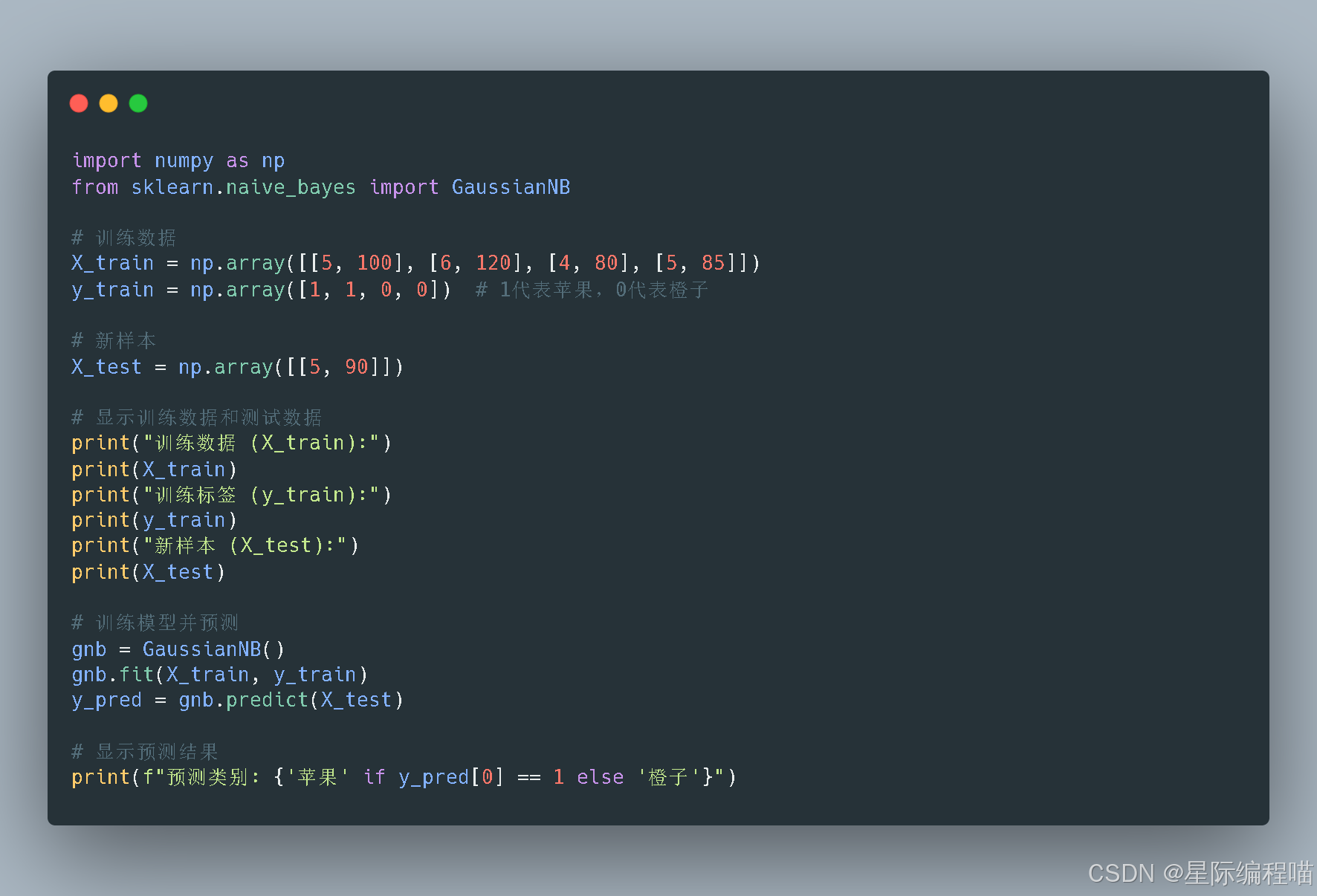
运行结果

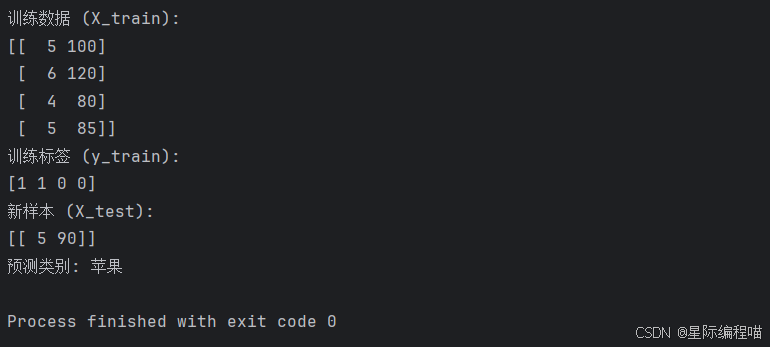
搞笑故事

有一天，包青天正忙于断案，忽然接到一个离奇举报。举报人称村里的李大妈不仅煮得一手好土豆汤，还能凭借那秘制汤料判断谁是好人谁是坏人。包青天心中暗想，李大妈的土豆汤难道隐藏着某种神秘的统计秘诀？他决定一探究竟，将李大妈的“汤理”与现代机器学习算法GaussianNB相结合。

GaussianNB是一种基于高斯分布和朴素贝叶斯原理的分类工具。它的精髓在于将数据中的每个特征视为独立变量，通过计算各特征在不同类别下出现的概率，进而判断数据点更可能属于哪一类。包青天打趣道，若将李大妈土豆汤中各式调料、火候、煮制时间等视为数据特征，那么每一碗汤的风味就仿佛一个数据点，而李大妈凭直觉做出的判断就像是GaussianNB经过精密计算后的分类结果。

为了验证这一奇思妙想，包青天暗中收集了村中数十碗土豆汤样本，每碗汤记录下调料比例、煮汤时间等关键数据，并标注当时品尝者的“好人”或“坏人”标签。随后，他用GaussianNB对这些数据进行训练，通过高斯分布模型计算每种调料在好人与坏人中的均值和标准差，再利用贝叶斯定理推算出各个特征的后验概率。模型计算过程既迅速又精确，就像包青天审案时那样，层层剥茧抽丝，最终给出了令人信服的预测结果。

结果显示，GaussianNB准确地重现了李大妈的判断，仿佛这位老奶奶的秘制土豆汤背后竟蕴藏着高深的数学原理。村民们纷纷感叹，原来古老的智慧与现代科技竟能如此默契配合。李大妈的汤理不再仅仅是传说，而被科学解释为通过“高斯分布”捕捉了人性的微妙差异。包青天借助GaussianNB的神奇力量，不仅解决了村中的纷争，也为大家呈现了一场跨越古今的智慧对话。此案既充满幽默趣味，又展示了数据科学在现实生活中的妙用，让每个人都在欢笑中感受到科学的严谨与魅力。

常见问题

1.GaussianNB 的假设是什么？

高斯朴素贝叶斯假设每个特征在给定类别的条件下，服从高斯分布。

2.GaussianNB 可以处理缺失数据吗？

高斯朴素贝叶斯不能直接处理缺失数据，需先进行数据填充。

3.GaussianNB 适用于哪些数据类型？

它适用于数值型数据，尤其是当数据符合高斯分布时，表现尤为优秀。

适用场景

文本分类：例如垃圾邮件识别。

医学诊断：根据症状预测疾病类型。

金融风控：如信用卡欺诈检测。

注意事项

• 特征之间的独立性假设：GaussianNB 假设特征是相互独立的，这在现实中往往不完全成立，但它仍然能取得不错的效果。
• 对噪声敏感：高斯朴素贝叶斯对数据中的噪声较为敏感，数据清洗非常重要。

最佳实践

• 在使用 GaussianNB 时，确保数据接近高斯分布。可以通过数据可视化来观察数据的分布特性。
• 尽量对数据进行预处理和特征工程，以提高模型的表现。
• 在高维数据集上，使用降维技术（如 PCA）来减少噪声。

总结

GaussianNB不仅是一个高效的分类算法，它更像是包青天在数据世界中的化身，凭借精湛的“审案武功”，迅速从复杂的数据中找出最有可能的分类答案。它拥有的贝叶斯定理和高斯分布就像是包大人手中的审案大典，简洁而高效。面对错综复杂的案件，包青天总能凭借简洁的推理做出精准的判断，而GaussianNB也一样，能够在数据海洋中迅速筛选出重要信息，给出清晰、可靠的分类结果。

就像包青天审案时不需要依赖复杂的证据，而是依靠强大的推理力和逻辑判断，GaussianNB在处理分类任务时，也不需要复杂的计算，只依靠简明的数学公式，便能快速得出答案。特别是当特征独立且符合高斯分布时，GaussianNB的“功力”如同包青天的审案速度，既迅速又准确。

它在大规模数据的处理上，速度极快，资源消耗小，简直就像江湖中的“轻功大师”，一跃而过，不留痕迹。无论面对多么复杂的分类任务，GaussianNB总能为你提供如包青天断案般迅速而又精准的答案，成为你数据分类道路上的得力助手。