数据结构与算法二叉搜索树,使用TreeMap将键值对存储在一棵二叉搜索树的节点

目录
数据结构与算法——二叉搜索树,使用TreeMap将键值对存储在一棵二叉搜索树的节点
二叉搜索树
【 二叉搜索树 (BST)】:对于树中的每个节点,其 左子树的每个节点 的值都要小于这个节点的值, 右子树的每个节点 的值都要大于这个节点的值。 左小右大 。 中序遍历结果是有序的 ,会从小到大排序。
7
/ \
4 9
/ \ \
1 8 10 (不符合)可以使用
TreeMap
把键值对存储在一棵二叉搜索树的节点里
通过遍历这棵二叉搜索树,比遍历普通的二叉树能更快实现增删查改
class TreeNode {
constructor(key, value) {
this.key = key;
this.value = value;
this.left = null;
this.right = null;
this.size = 1;
}
}1. 常用操作:
其中包括:
【插入或更新键值对】
【获取键对应的值】
【检查是否包含键】
【返回所有键的有序集合】
【找到最小/最大键】
【找到小于等于key的最大键/大于等于key的最小键】
【区间查询】
class MyTreeMap {
constructor() {
this.root = null;
}
_size(node) {
return node ? node.size : 0;
}
//插入或更新键值对
put(key, value) {
//根节点
this.root = this._put(this.root, key, value);
}
_put(node, key, value) {
if (node === null) {
return new TreeNode(key, value);
}
if (key < node.key) {
node.left = this._put(node.left, key, value);
}else if (key > node.key) {
node.right = this._put(this.right, key, value);
}else {
node.value = value;
}
node.size = 1 + this._size(node.left) + this._size(node.right);
return node;
}
//获取键对应的值
get(key) {
let node = this.root;
while (node !== null) {
if (key < node.key) {
node = node.left;
}else if (key > node.key) {
node = node.right;
}else {
return node.value;
}
}
return false;
}
//检查是否包含键
containKey(key) {
let node = this.root;
while (node !== null) {
if (key < node.key) {
node = node.left;
}else if (key > node.key) {
node = node.right;
}else {
return true;
}
}
return false;
}
//返回所有键的有序集合
keys() {
const result = [];
this._inOrder(this.root, result);
return result;
}
_inOrder(node, result) {
if (node === null) { return; }
this._inOrder(node.left, result);//左
result.push(node.key);//中
this._inOrder(node.right, result);//右
}
//找到最小键
firstKey() {
let node = this.root;
while (node && node.left !== null) { node = node.left;}
return node ? node.key : null;
}
//找到最大键
lastKey() {
let node = this.root;
while (node && node.right !== null) { node = node.right;}
return node ? node.key : null;
}
//小于等于key的最大键
//分两种情况: 节点key的值===要查找的key值; 节点key的值大于要查找的值
min_maxKey() {
let node = this.root;
let data = null;
while (node !== null) {
if (node.key === key) return key;
if (node.key > key ){
node = node.left;
}else {
data = node.key;
node = node.right;
}
}
return data;
}
//大于等于key的最小值
max_minKey() {
let node = this.root;
let data = null;
while (node !== null) {
if (node.key === key ) return key;
if (node.key < key) {
node = node.right;
}else {
data = node.key;
node = node.left;
}
}
return data;
}
//区间查询
rangeKeys(low, high) {
const result = [];
this._rangeKeys(this.root, low, high, result);
return result;
}
_rangeKeys(node, low, high, result) {
if (node === null) return;
if (low < node.key) {
this._rangeKeys(node.left, low, high, result);
}
if (node.key >= low && node.key <= high) {
result.push(node.key);
}
if (node.key < high) {
this._rangeKeys(node.right, low, high, result);
}
}
}2. 理解删除操作
【 删除键 】
// 核心:
// 二叉搜索树的性质:左子树所有节点 < 当前节点 < 右子树所有节点
// 寻找要删除键A的右子树中最小值节点B,并替代A,然后删除B节点
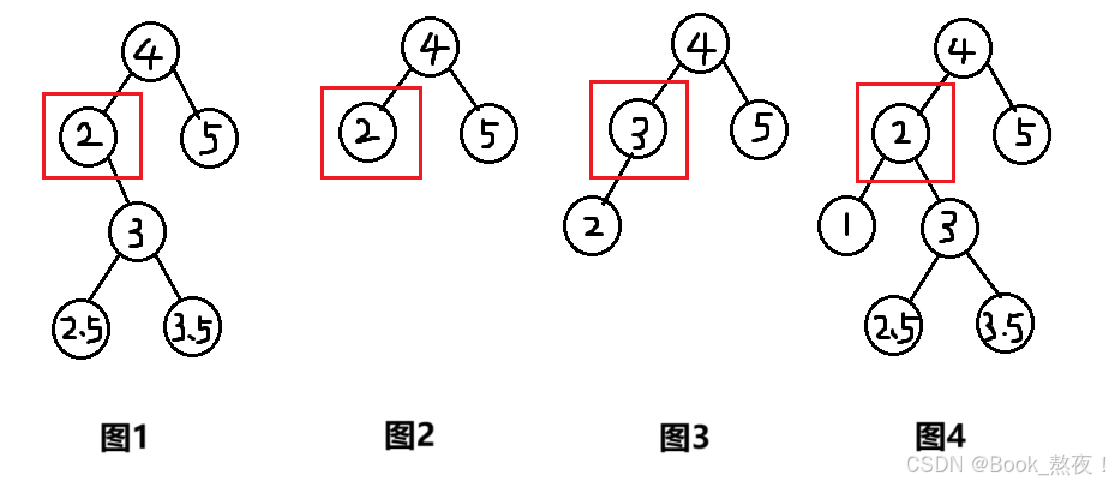
分为以下情况:
假设红色框中节点待删除,为键A
图1、图2对应键A左子树为null,图三对应J键A右子树为null,图四对应键A左右子树都不为null
//删除键
// 核心:
// 二叉搜索树的性质:左子树所有节点 < 当前节点 < 右子树所有节点
// 寻找要删除键A的右子树中最小值节点B,并替代A,然后删除B节点
remove(key) {
this.root = this._remove(this.root, key);
}
_remove(node, key) {
if (node === null) { return false;}
//递归搜索,直到找到key
if (key < node.key) {
node.left = this._remove(node.left, key);
}else if (key > node.key) {
node.right = this._remove(node.right, key);
}else {//找到key
if (node.left === null) { return node.right;}
if (node.right === null) { return node.left;}
const minNode = this._min(node.right);
node.key = minNode.key;
node.value = minNode.value;
node.right = this._deleteMin(node.right);
}
node.size = 1 + this._size(node.left) + this._size(node.right);
return node;
}
_min(node) {
while (node.left !== null) { node = node.left;}
return node;
}
_deleteMin(node) {
//当左子树为空时,直接将该节点的右子树返回,即删除了该节点
if (node.left === null) {return node.right;}
node.left = this._deleteMin(node.left);
node.size = 1 + this._size(node.left) + this._size(node.right);
return node;
}