刷题记录-贪心-23968.-监控二叉树

目录
刷题记录 贪心-23:968. 监控二叉树
题目:
难度:困难
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视 其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
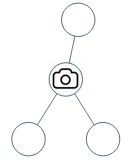
输入:[0,0,null,0,0]
输出:1
解释:如图所示,一台摄像头足以监控所有节点。示例 2:
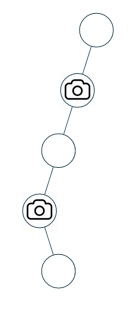
输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。提示:
- 给定树的节点数的范围是
[1, 1000]。 - 每个节点的值都是 0。
一、模式识别
1.二叉树
二叉树类的题目的第一问题就是确定遍历顺序:这是极其重要的一点
检视节点 》 能同时考虑到左右孩子 》 后序
2.贪心
(1)定义三个状态: 暗节点, 监视器(灯),亮节点(被照亮)
代码实现:用哈希表记录信号强度,参照MC的红石电路,设定信号强度为2,每次衰减1
不在哈希表内:暗节点
值为2:监视器(灯)
值为1:亮节点(被照亮)
(2)如何放监视器并维护哈希表
①判断是否放置监视器的条件:有暗孩子(有孩子,且至少有一个暗节点孩子)
②如果有孩子是监视器,则设定本节点为亮节点
(3)贪心算法可能无法照顾到根节点
容易忽略的是这个方法容易把根节点略过根节点,
这个需要在代码最后打个补丁
二、代码实现
统一迭代法骨架 + 贪心判断:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minCameraCover(self, root: Optional[TreeNode]) -> int:
if not root.left and not root.right: return 1
ans = 0
stk = [root]
cache = {}
while stk:
node = stk.pop()
if node:
stk.append(node)
stk.append(None)
if node.right: stk.append(node.right)
if node.left: stk.append(node.left)
else:
node = stk.pop()
if (node.left and node.left not in cache) or (node.right and node.right not in cache):
cache[node] = 2
ans += 1
elif (node.left and cache[node.left] == 2) or (node.right and cache[node.right] == 2):
cache[node] = 1
if root not in cache: ans += 1
return ans指针迭代法骨架 + 贪心判断:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def minCameraCover(self, root: Optional[TreeNode]) -> int:
if not root.left and not root.right: return 1
stk, node, prev = [], root, None
cache = {}
ans = 0
while stk or node:
while node:
stk.append(node)
node = node.left
node = stk.pop()
if not node.right or node.right == prev:
if (node.left and node.left not in cache) or (node.right and node.right not in cache):
cache[node] = 2
ans += 1
elif (node.left and cache[node.left] == 2) or (node.right and cache[node.right] == 2):
cache[node] = 1
prev = node
node = None
else:
stk.append(node)
node = node.right
if root not in cache: ans += 1
return ans递归:略,本题需要最后对根节点打补丁,用递归需要辅助函数,写起来比较繁琐