2025.3.10-2025.3.16学习周报

2025-03-16 约 3367 字预计阅读 7 分钟

https://bing.ee123.net/img/rand?artid=146296770

2025.3.10–2025.3.16学习周报

摘要

在本周阅读的论文中，提出了一种名为PI-SGTGCN的模型。PI-SGTGCN通过结合S- GCN与FD信息，成功捕捉了数据中复杂的空间和时间依赖性。相较于传统的静态图方法，PI- SGTGCN的主要优势在于动态图邻接矩阵的构建，其采用空间注意力机制，从而使得模型有更强的适应性。模型采用多时间尺度编码策略提取长短期周期特征，并结合GRU- Transformer双路径架构分别建模交通流的局部波动与全局周期性，从而有效平衡了突发事件的瞬态响应与规律性模式的稳态表达。PI- SGTGCN凭借其创新的结构设计和物理信息的融入，显著提高了预测的准确性和鲁棒性，为时序预测领域提供了一种高效的解决方案。

Abstract

In the paper read this week, a model called PI-SGTGCN was proposed. PI-SGTGCN successfully captures the complex spatial and temporal dependencies in data by combining spatiotemporal graph convolutional networks with Fundamental Diagram information. Compared to traditional static graph methods, the main advantage of PI-SGTGCN lies in the construction of dynamic graph adjacency matrix, which adopts spatial attention mechanism to make the model more adaptable. The model adopts a multi time scale encoding strategy to extract long and short-term periodic features, and combines the GRU-Transformer dual path architecture to model the local fluctuations and global periodicity of traffic flow, effectively balancing the transient response of emergencies with the steady- state expression of regular patterns. PI-SGTGCN, with its innovative structural design and integration of physical information, significantly improves the accuracy and robustness of predictions, providing an efficient solution for the field of time series prediction.

1 文献阅读

本周阅读了一篇名为“Spatial-temporal graph convolution network model with traffic fundamental diagram information informed for network traffic flow prediction”的论文论文地址：在论文中作者提出了一种名为PI-SGTGCN的模型，PI- SGTGCN模型通过结合空间注意机制的GCN、GRU和Transformer，成功捕捉了交通流量的时空特征，并利用FD信息增强了长期预测的准确性。

1.1 GCN

GCN实际上跟CNN的作用一样，就是一个特征提取器，只不过它的对象是图数据。GCN精妙地设计了一种从图数据中提取特征的方法，从而让我们可以使用这些特征去对图数据进行节点分类（node classification）、图分类（graph classification）、边预测（link prediction），还可以顺便得到图的嵌入表示（graph embedding）。初期研究者为了从数学上严谨的推导GCN公式是有效的，所以会涉及到诸如傅里叶变换，拉普拉斯。GCN的卷积核更小，参数量也更少，计算复杂度也随之变小了，它等价于最简的一阶切比雪夫卷积。假设有一个图数据，一共有N个节点（node），每个节点都有自己的特征，我们设这些节点的特征组成一个N×D维的矩阵X，然后各个节点之间的关系也会形成一个N×N维的矩阵A，也称为邻接矩阵（adjacency matrix）。X和A便是我们模型的输入。下图就是GCN网络层的基础公式，这个式子的意思就是，先把node feature（x)mm经过一个transform，把所有的邻居节点以及它自己本身加起来取平均值，再加一个b经过一个activation之后就会得到最后的hv。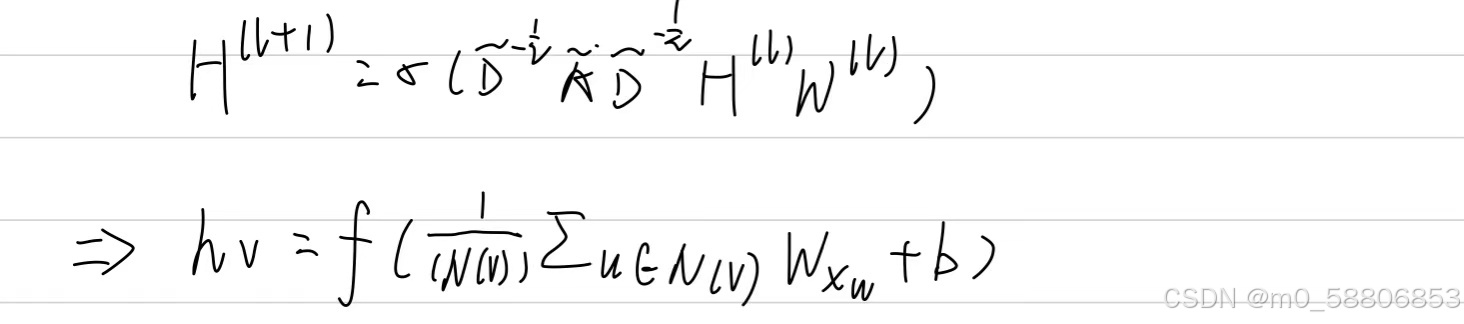通过一个例子对公式原理进行分析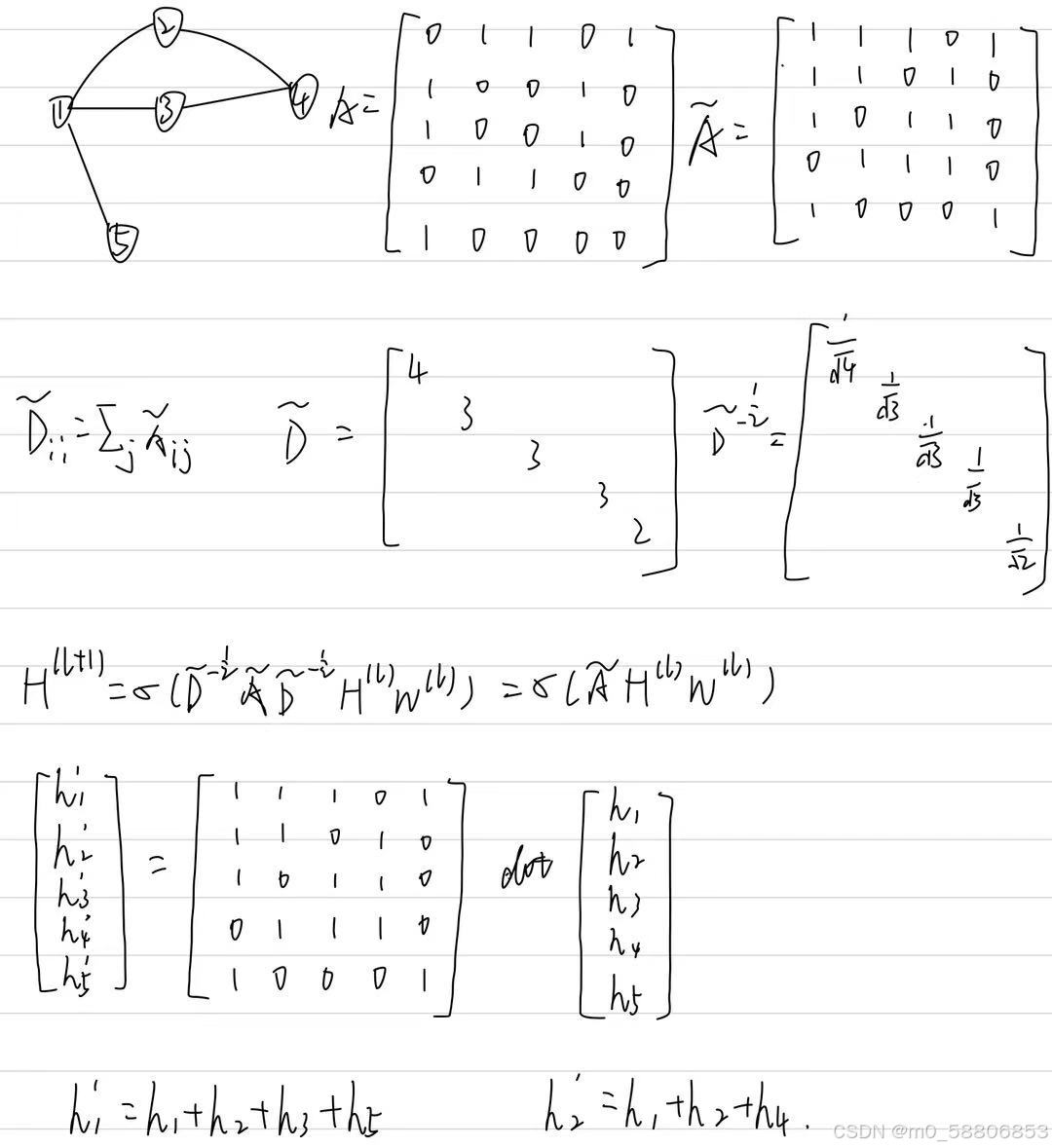下一层某一节点的向量表示就是当前层节点向量表示的和，这其实是一个消息传递的过程，经这样消息传递的操作后，下一层的节点就聚集了它一阶邻居与自身的信息。这就很有效的保留了图结构给我们承载的信息。因此AHI的含义即聚合周围节点的信息，来更新自己。而简单的聚合却不太合理，因为不同的节点重要性不一样，如果一个节点的「度」非常大，即与他相邻的节点非常多，那么它传递的消息，权重就应该小一点。对于度矩阵D，其数值就是代表一个节点的邻居节点数量，所以乘以度矩阵的逆也就是稀释掉度很大的节点的重要度。 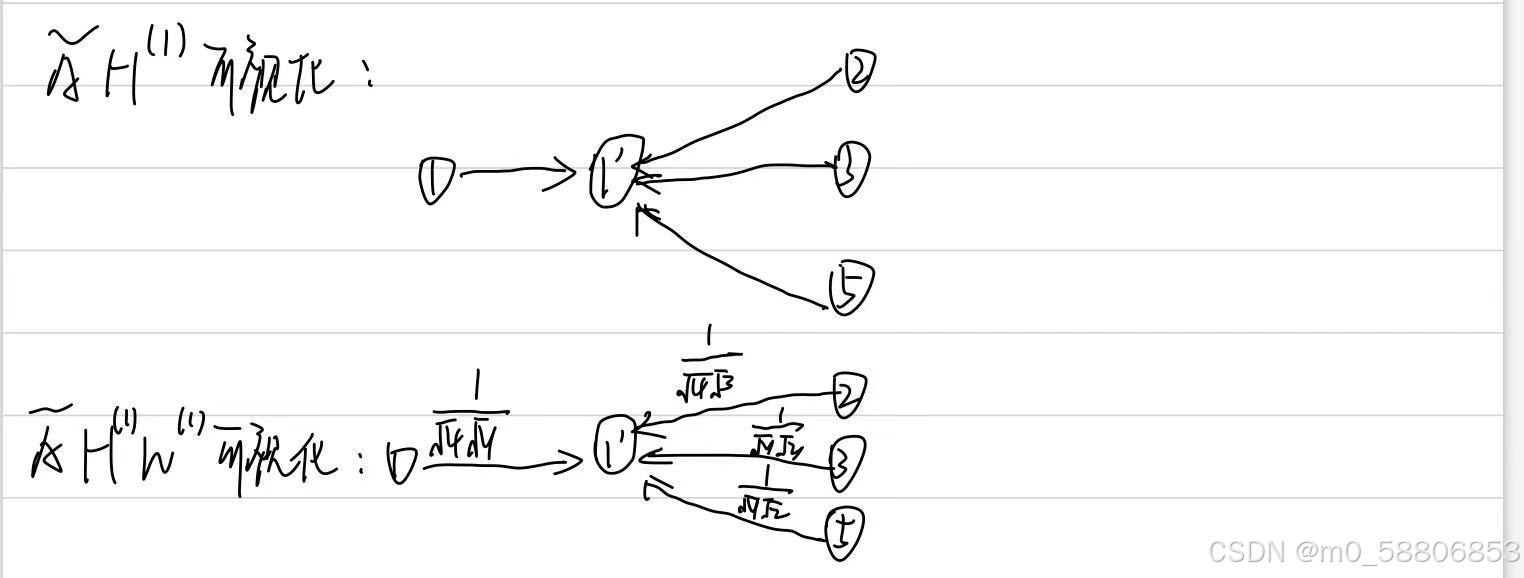GCN也是一个神经网络层，这里的权重是所有节点共享的，类比于CNN中的参数共享；另外可以将节点的邻居节点看成感受野，随着网络层数的增加，感受野越来越大，即节点的特征融合了更多节点的信息。直观的图卷积示意图如下：每一层GCN的输入都是邻接矩阵A和node的特征H，再乘一个参数矩阵W，然后激活一下，这就相当于一个简单的神经网络层，但是这种做法存在局限性。以下是GCN公式推导的代码实现： import numpy as np from scipy.linalg import fractional_matrix_power A=np.mat(‘0,1,1,1,0,0;1,0,1,0,0,0;1,1,0,0,1,1;1,0,0,0,0,0;0,0,1,0,0,1;0,0,1,0,1,0’) print(A) D=np.mat(‘3,0,0,0,0,0;0,2,0,0,0,0;0,0,4,0,0,0;0,0,0,1,0,0;0,0,0,0,2,0;0,0,0,0,0,2’) print(D)

print(D**(-1))

D_half=fractional_matrix_power(D,0.5)

print(D_half)

D_half_neg=fractional_matrix_power(D,-0.5)

print(D_half_neg)

A_row=np.matmul(D**(-1),A)

print(A_row)

Eigen_values,Eigen_vectors=np.linalg.eig(A_row)#计算特征值

print(Eigen_values)

A_col=np.matmul(A,D**(-1))

print(A_col)

Eigen_values,Eigen_vectors=np.linalg.eig(A_col) print(Eigen_values) A_naive=D**(-1) @ A @ D**(-1) print(A_naive) Eigen_values,Eigen_vectors=np.linalg.eig(A_naive) print(Eigen_values) A_sym=D_half_neg @ A @ D_half_neg #保证了特征值的归一化最大特征值始终为1 print(A_sym) V,D=np.linalg.eig(A_sym) print(V)

1.2 模型框架

论文提出的PI- SGTGCN模型模型的核心思想是通过多组件协同架构，结合动态图结构、物理规律与深度学习技术，实现对复杂交通网络时空依赖关系的多层次解耦与建模。其结构如下图所示：从结构设计来看，模型首先通过多模式编码层提取交通数据的周期性特征，将历史数据按周、日、小时三种时间尺度切片并融合，以捕捉交通流的长期、中期与短期周期模式。这种多时间尺度的特征融合策略为后续模型提供了丰富的时序上下文信息。 S-GCN层采用空间注意力机制构建动态图邻接矩阵，突破传统GCN依赖静态邻接矩阵的局限，使模型能够感知随环境因素（如事故、天气）动态变化的空间关联强度。模型将交通基本图的物理特征嵌入邻接矩阵的对角线元素，这种物理信息与数据驱动模型的融合机制，既保留了节点自身静态属性，又增强了模型对交通流演化本质规律的理解。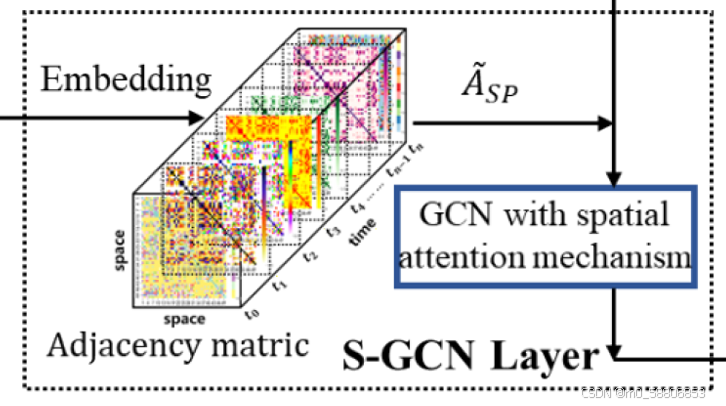除此，模型通过使用GRU- Transformer双路径时序层来平衡局部时序动态与全局周期模式的捕捉能力。GRU路径通过门控机制建模短期连续依赖，其隐藏状态传递机制特别适合处理分钟级预测任务中的瞬态变化。Transformer路径则利用多头自注意力机制捕获长时程周期性和突发事件引发的时序异常。双路径输出通过可学习的权重矩阵进行动态融合，使得模型能够根据预测跨度（短期/长期）自适应调整局部细节与全局模式的贡献度。该模型的算法实现如下所示：其核心逻辑是训练前从历史数据中拟合交通基本图（FD）参数（如自由流速度），将其编码到图邻接矩阵的对角线，使图卷积同时学习空间关联与物理规律。然后先冻结图卷积层参数，训练时序模块（GRU- Transformer）捕捉纯时间依赖，再联合微调用。每10个epoch用最新模型隐藏状态重新计算节点间注意力权重，通过滑动平均平衡动态适应与稳定性，使图结构既能响应突发事件，又不会过度震荡。

1.3 实验分析

（1）数据集 实验数据使用加利福尼亚州交通部（Caltrans）的PeMS（Performance Measurement System）数据集。选取PeMS中District 7的数据，包含多个交通检测站点的流量、速度和时间占用率等信息。 （2）评估标准 MAE: MAPE: RMSE: 论文通过与包括ARIMA、SVR、GRU、Transformer、GCN、GAT、STGCN、ASTGCN和STGNN在内的基线模型的预测结果相比较体现PI- SGTGCN的先进性。 （3）实验结果 PI-SGTGCN在短、中、长期交通预测任务中均显著优于纯数据驱动模型（如DCRNN、STGCN）和传统物理启发式模型（如PINN- FD），尤其在30分钟以上的长期预测中优势更明显，表明物理信息与动态图协同机制能有效捕捉交通流的本质演化规律。实验结果如下图所示：为了显示各个站点的更多细节，研究进一步具体比较了 PI- SGTGCN、ASTGCN、STGCN和STGNN这四个表现最好的模型中每个站点的预测性能结果如下图所示：每个模型所包围的区域在很大程度上重叠，这表明模型之间的性能差异对于短期预测来说相对较小。这可以归因于涉及交通流模式中较少的未知和偶发性变化的预测，使其更易于建模。然而在30分钟和 60分钟的预测间隔内，PI-SGTGCN 所包围的区域明显小于其他模型。它表明 PI-SGTGCN 在长期预测任务中实现了性能改进，性能差距在 60 分钟时最为明显。原因是长期预测包含更复杂的流量变化，需要对错综复杂的时空信息进行解耦。为了研究两种测站类型预测结果的差异，下图显示了预测的可视化以及地面实况，重点是 60分钟的预测间隔。结果表明，PI-SGTGCN的预测结果与5号站的地面实况非常吻合。如框(a)和框(b)所示，与其他型号相比，PI-SGTGCN 表现出更强的捕获流量峰值波动的能力。此外，即使对于18 号站，PI-SGTGCN 的预测也与地面实况非常吻合。当交通流量发生剧烈变化时，与其他模型相比，PI-SGTGCN 仍然能够捕捉到交通流量演变的趋势。